Question

Cho biết tập hợp tất cả các giá trị của tham số m để phương trình 2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm là S = [ - a b ; + ∞ ) , với a, b là các số nguyên dương và  a b  là phân số tối giản. Tính T = a . b

A. T = -5.

B. T = 5.

C. T = 11.

D. T = 55

Answer 1

Đặt x + 1 t = t , t ≥ 2  khi đó phương trình trở thành 2 t 2 − 3 t − 5 m − 3 = 0    ( * )

Phương trình  2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn  t ≥ 2

Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): y = 2 t 2 − 3 t − 3 và đường thẳng d : y = 5 m

Xét parabol  P : y = 2 t 2 - 3 t - 3 ta có bảng biến thiên như sau:

 

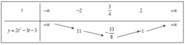
Từ bảng biến thiên ta có phương trình (*) có nghiệm  t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )  khi và chỉ khi  5 m ≥ - 1  hoặc  5 m ≥ 11

Vậy khi m ∈ − 1 5 ; + ∞ thì phương trình có nghiệm ⇒ a = 1 b = 5 ⇒ T = 5

Đáp án cần chọn là: B