Ta có: 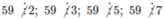
72 = 49 < 59, 112 = 121 ≥ 59
Vậy 59 là số nguyên tố
Ta có: 121 /⋮ 2; 121 /⋮ 3; 121 /⋮ 5; 121 /⋮ 7; 121 ⋮ 11
Vậy 121 là hợp số
Tương tự ta có 179; 197 và 217 là các số nguyên tố
Ta có: 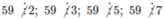
72 = 49 < 59, 112 = 121 ≥ 59
Vậy 59 là số nguyên tố
Ta có: 121 /⋮ 2; 121 /⋮ 3; 121 /⋮ 5; 121 /⋮ 7; 121 ⋮ 11
Vậy 121 là hợp số
Tương tự ta có 179; 197 và 217 là các số nguyên tố
Cho biết: Nếu số tự nhiên a (lớn hơn 1) không chia hết cho mọi số nguyên tố p mà bình phương không vượt quá a (tức là p2 ≤ a) thì a là số nguyên tố. Dùng nhận xét trên cho biết số nào trong các số ở bài 153 là số nguyên tố?
153. Điền vào bảng sau mọi số nguyên tố mà p2 \(\le a\)
| a | 59 | 121 | 179 | 197 | 217 |
| p |
156 . Cho biết : nếu số tự nhiên a ( lớn hơn 1 ) không chia hết cho mọi nguyên tố p mà bình phương không vượt quá a ( tức là \(p^2\le a\)) thì a là số nguyên tố. Dùng nhận xét trên cho biết số nào trong các số a ở bài 153 là số nguyên tố ?
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
1, Số tận cùng là 4 thì chia hết cho 2
2, Số chia hết cho 2 thì có chữ số tận cùng là 4
3, Số chia hết cho 5 thì có chữ số tận cùng là 5
4, Nếu một số hạng của tổng không chia hết cho 7 thì tổng không chia hết cho 7
5, Số chia hết cho 9 có thể chia hết cho 3
6, Số chia hết cho 3 có thể chia hết cho 9
7, Nếu một số không chia hết cho 9 thì tổng các chữ số của nó không chia hết cho 9
8, Nếu tổng các chữ số của số a chia hết cho 9 dư r thì số a chia hết cho 9 sư r
9, Số nguyên là số tự nhiên chỉ chia hể cho 1 và chính nó
10, Hợp số là số tự nhiên nhiều hơn 2 ước
11, Một số nguyên tố đều là số lẻ
12, không có số nguyên tố nào có chữ số hàng đơn vị là 5
13, Không có số nguyên tố lớn hơn 5 có chữ số tạn cùng là 0; 2; 4; 5; 6; 8
14, Nếu số tự nhiên a lớn hơn 7 và chia hết cho 7 thì a là hợp số
15, Hai số nguyên tố cùng nhau là hai số cùng nhau là số nguyên tố
16, Hai số nguyên tố là hai số nguyên tố cùng nhau
17, Hai số 8 và 25 là hai số nguyên tố cùng nhau
Điền vào bảng sau mọi số nguyên tố p mà bình phương của nó không vượt quá a tức là p2 ≤ a:
| a | 29 | 67 | 49 | 127 | 173 | 253 |
| p | 2, 3, 5 |
Cho số tự nhiên n lớn hơn hoặc bằng 2. gọi p1, p2, ... ,pn là những số nguyên tố sao cho pn nhỏ hơn hoặc bằng n + 1. đặt A = p1 . p2 . ... . pn. Chứng minh rằng trong dãy số các số nguyên tố liên tiếp A + 2, A +3, ... , A + (n + 1) không chứa 1 số nguyên tố nào
Bài 1 ( Dạng 1): Cho p là số nguyên tố và 2 số 8p -1; 8p + 1 là số nguyên tố. Hỏi số thứ 3 là số nguyên tố hay hợp số
Bài 2 ( Dạng 1): Tìm số tự nhiên k để dãy k + 1, k + 2,…,k + 10 chứa nhiều số nguyên tố nhất
Bài 3 ( Dạng 2): Tìm số nhỏ nhất A có 6 ước; 9 ước
Bài 4 ( Dạng 2): Chứng minh rằng: (p – 1)! chia hết cho p nếu p là hợp số, không chia hết cho p nếu p là số nguyên tố.Bài 5 ( Dạng 2): Cho 2m – 1 là số nguyên tố. Chứng minh rằng m cũng là số nguyên tố
Bài 6 ( Dạng 2): Chứng minh rằng: 2002! – 1 có mọi ước số nguyên tố lớn hơn 2002
Bài 7 ( Dạng 3): Tìm n là số tự nhiên khác 0 để:
a) n4+ 4 là số nguyên tố
b) n2003+n2002+1 là số nguyên tố
Bài 8 ( Dạng 3): Cho a,b,c,d thuộc N* thỏa mãn ab = cd. Chứng tỏ rằng số A = an+bn+cn+dn là hợp số với mọi số tự nhiên n
Bài 9 ( Dạng 4): Tìm số nguyên tố p sao cho 2p+1 chia hết cho p
Bài 10 ( Dạng 4): Cho p là số nguyên tố lớn hơn 2. Chứng tỏ rằng có vô số số tự nhiên n thỏa mãn n.2n -1 chia hết cho p
24 Khẳng định nào sau đây là sai?
A Số 0 và số 1 không phải là số nguyên tố cũng không phải là hợp số.
B. Cho số tự nhiên a1, a có 2 ước thì a là hợp số.
C. Số 2 là số nguyên tố chẵn duy nhất.
D. Số nguyên tố là số tự nhiên lớn hơn 1 mà chỉ có hai ước 1 và chính nó
Bài 1 ( Dạng 1): Cho p là số nguyên tố và 2 số 8p -1; 8p + 1 là số nguyên tố. Hỏi số thứ 3 là số nguyên tố hay hợp số
Bài 2 ( Dạng 1): Tìm số tự nhiên k để dãy k + 1, k + 2,…,k + 10 chứa nhiều số nguyên tố nhất
Bài 3 ( Dạng 2): Tìm số nhỏ nhất A có 6 ước; 9 ước
Bài 4 ( Dạng 2): Chứng minh rằng: (p – 1)! chia hết cho p nếu p là hợp số, không chia hết cho p nếu p là số nguyên tố.Bài 5 ( Dạng 2): Cho 2m – 1 là số nguyên tố. Chứng minh rằng m cũng là số nguyên tố
Bài 6 ( Dạng 2): Chứng minh rằng: 2002! – 1 có mọi ước số nguyên tố lớn hơn 2002 ( Đây là bài của chịnhunglth đó ạ)
Bài 7 ( Dạng 3): Tìm n là số tự nhiên khác 0 để:
a) n4+ 4 là số nguyên tố
b) n2003+n2002+1 là số nguyên tố
Bài 8 ( Dạng 3): Cho a,b,c,d thuộc N* thỏa mãn ab = cd. Chứng tỏ rằng số A = an+bn+cn+dn là hợp số với mọi số tự nhiên n
Bài 9 ( Dạng 4): Tìm số nguyên tố p sao cho 2p+1 chia hết cho p
Bài 10 ( Dạng 4): Cho p là số nguyên tố lớn hơn 2. Chứng tỏ rằng có vô số số tự nhiên n thỏa mãn n.2n -1 chia hết cho p
Các bạn có thể trả lời vài câu hỏi cũng được.Bạn nào trả lời được nhiều mình sẽ ủng hộ cho nha
a) Cho n là số nguyên tố không chia hết cho 3. Chứng minh rằng n 2 chia cho 3 dư 1.
b) Cho p là một số nguyên tố lớn hơn 3. Hỏi p 2 + 2003 là số nguyên tố hay hợp số