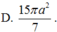Hướng dẫn giải:
Ta có: $x^3 . 2^x+2^{x+1}\left(y^3-68-2^{\frac{4 z+y-x}{2}}\right)+2^{x+4 z}=\ln \dfrac{1}{(e^2)^y}$
$\Leftrightarrow x^3+2\left(y^3-68-2 \dfrac{4 z+y-x}{2}\right)+2^{4 z}+2^{y-x}=0$
$\Leftrightarrow\left(2^{2 z}-2^{\frac{y-x}{2}}\right)^2+x^3+2 y^3-136=0$ (1)
Lại có: $x^3+2 y^3 \geq\left(18-y^2\right)^3+2 y^3 \geq 136 \Rightarrow\left(2^{2 z}-2^{\frac{y-x}{2}}\right)^2+x^3+2 y^3-136 \geq 0$ (2)
Từ (1), (2) ta suy ra được $x=2$, $y=4$, $z=\dfrac{1}{2} \Rightarrow \log _z(x y)=-3$.