a) Vì C M A = D M B = 60 o ⇒ C M B = D M A = 120 o . Xét ∆ CMB và ∆ AMD có
C M = A M C M B = D M A ⇒ Δ C M B = Δ A M D ( c . g . c ) M B = M D ⇒ M C B = M A D M B C = M D A
Suy ra AMPC và BMPD là các tứ giác nội tiếp

a) Vì C M A = D M B = 60 o ⇒ C M B = D M A = 120 o . Xét ∆ CMB và ∆ AMD có
C M = A M C M B = D M A ⇒ Δ C M B = Δ A M D ( c . g . c ) M B = M D ⇒ M C B = M A D M B C = M D A
Suy ra AMPC và BMPD là các tứ giác nội tiếp
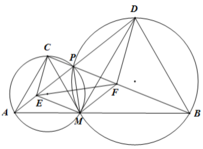
Cho ba điểm A, M, B phân biệt, thẳng hàng và M nằm giữa A, B. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, dựng hai tam giác đều AMC và BMD. Gọi P là giao điểm của AD và BC.
c) Đường thẳng nối tâm của hai đường tròn ngoại tiếp hai tứ giác AMPC và BMPD cắt PA, PB tương ứng tại E, F. Chứng minh CDFE là hình thang.
Cho ba điểm A, M, B phân biệt, thẳng hàng và M nằm giữa A, B. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, dựng hai tam giác đều AMC và BMD. Gọi P là giao điểm của AD và BC.
b) Chứng minh C P . C B + D P . D A = A B
c) Đường thẳng nối tâm của hai đường tròn ngoại tiếp hai tứ giác AMPC và BMPD cắt PA, PB tương ứng tại E, F. Chứng minh CDFE là hình thang.
cho đoạn thẳng AB ( M khác A ; M khác B ) . Dựng về 1 phía của đường thẳng AB hai tam giác đều AMC và BMD. gọi P là giao điểm của AD và BC . 1) chứng minh AD= BC . 2) tứ giác AMPC và BMPD nội tiếp đường tròn
Cho đoạn thẳng AB và M là một điểm nằm giữa đoạn thẳng AB, trên cùng một nửa mặt phẳng bờ AB vẽ các hình vuông AMCD và BMEF. Gọi N là giao điểm thứ hai của đường tròn ngoại tiếp ∆AMC và ∆BME. Chứng minh A, E, N thẳng hàng
Cho đường tròn tâm O đường kính AB. Từ A và B vẽ hai dây cung AC và BD của đường tròn (O) cắt nhau tại N bên trong đường tròn (C,D nằm trên cùng nửa mặt phẳng bờ AB). Hai tiếp tuyến Cx, Dy của đường tròn (O) cắt nhau tại M. Gọi P là giao điểm của hai đường thẳng AD và BC
1. Chứng minh tứ giác DNCP nội tiếp đường tròn
2. Chứng minh ba điểm P, M, N thẳng hàng
Cho đường tròn (O) điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF).Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO)
a, Chứng minh MA. MB = ME.MF
b, Gọi H là hình chiêu vuông góc của điểm c lên đuờng thẳng MO. Chứng minh tứ giác AHOB nội tiếp
c, Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi S là giao điểm của hai đường thẳng CO và KF. Chứng minh các đường thẳng MS và KC vuông góc nhau
d, Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS và ABS và T là trung điểm của KS. Chứng minh ba điểm P, Q, T thẳng hàng
Cho đường tròn (O) có tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME<MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO).
a. Chứng minh rằng MA.MB = ME.MF
b. Gọi H là hình chiếu vuông góc của điểm C lên đường thẳng MO. Chứng minh tứ giác AHOB nội tiếp.
c. Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi S là giao điểm của hai đường thẳng CO và KF. Chứng minh rằng đường thẳng MS vuông góc với đường thẳng KC.
d. Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS và ABS và T là trung điểm của KS. Chứng minh ba điểm P, Q, T thẳng hàng.
Bài 5. Cho đường tròn (O) và một điểm M nằm bên ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB (A và B là tiếp điểm) và cát tuyến MNP (N nằm giữa M và P) với đường tròn . Gọi E là trung điểm của NP a) Chứng minh rằng năm điểm M, A, K, O, B cùng nằm trên một đường tròn, từ đó chứng minh KM là tia phân giác của AKB b) Gọi Q là giao điểm thứ hai của đường thẳng BK với đường tròn (O).Chứng minh AQ//NP c) Gọi H là giao điểm của AB và MO. Chứng minh rằng: MH.MO= MB2 ; MH.MO= MN.MP d) Chứng minh tứ giác NHOP nội tiếp e) Gọi E là giao điểm của AB và KO, F là giao điểm của AB và NP. CMR: AB2=4 HE.HF và tứ giác KEMH nội tiếp f) Chứng minh: EN, EP là các tiếp tuyến của (O)
): Cho đoạn thẳng AB = 2a có trung điểm O . Trên cùng một nửa mặt phẳng bờ AB , dựng nửa đường tròn (O,AB) và ( O’,AO) , Trên (O’) lấy M ( M ≠ A, M ≠ O ). Tia OM cắt (O) tại C . Gọi D là giao điểm thứ hai của CA với (O’). a/ Chứng minh rằng tam giác AMD cân . b/ Tiếp tuyến C của (O) cắt tia OD tại E. Xác định vị trí tương đối của đương thẳng EA đối với (O) và (O’). c/ Đường thẳng AM cắt OD tại H, đường tròn ngoại tiếp tam giác COH cắt (O) tại điểm thứ hai là N. Chứng minh ba điểm A, M, N thẳng hàng. d/ Tại vị trí của M sao cho ME // AB hãy tính OM theo a .