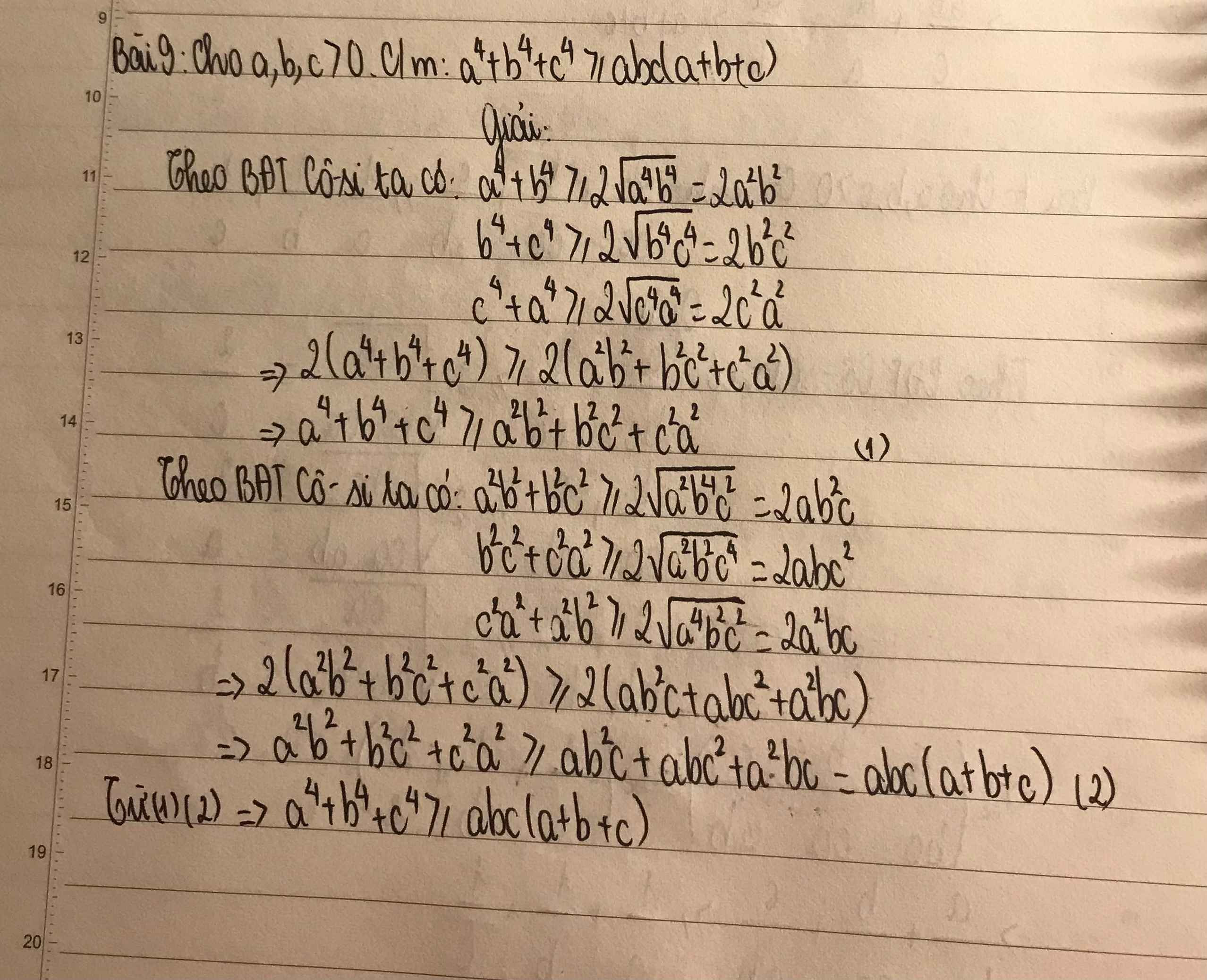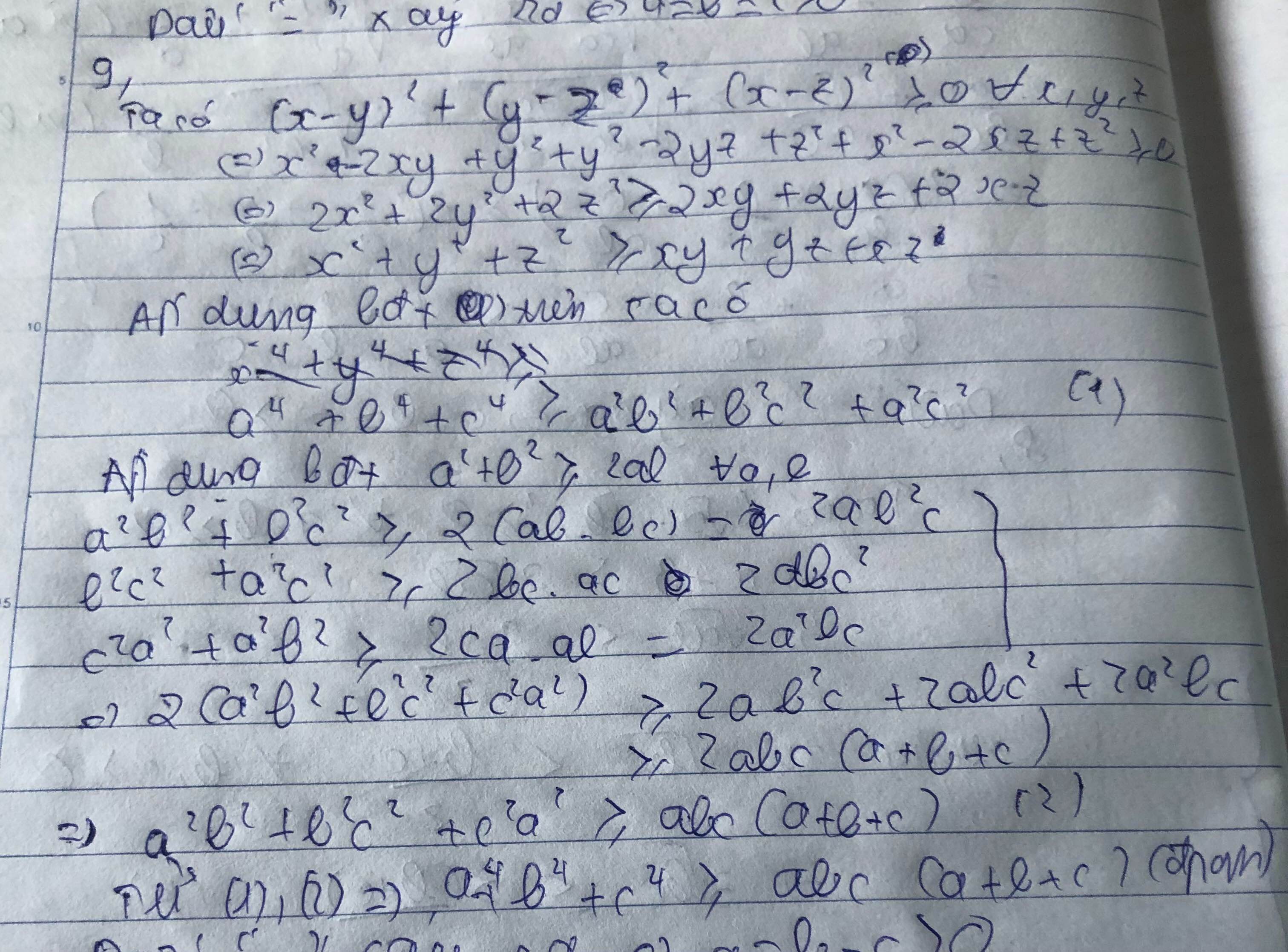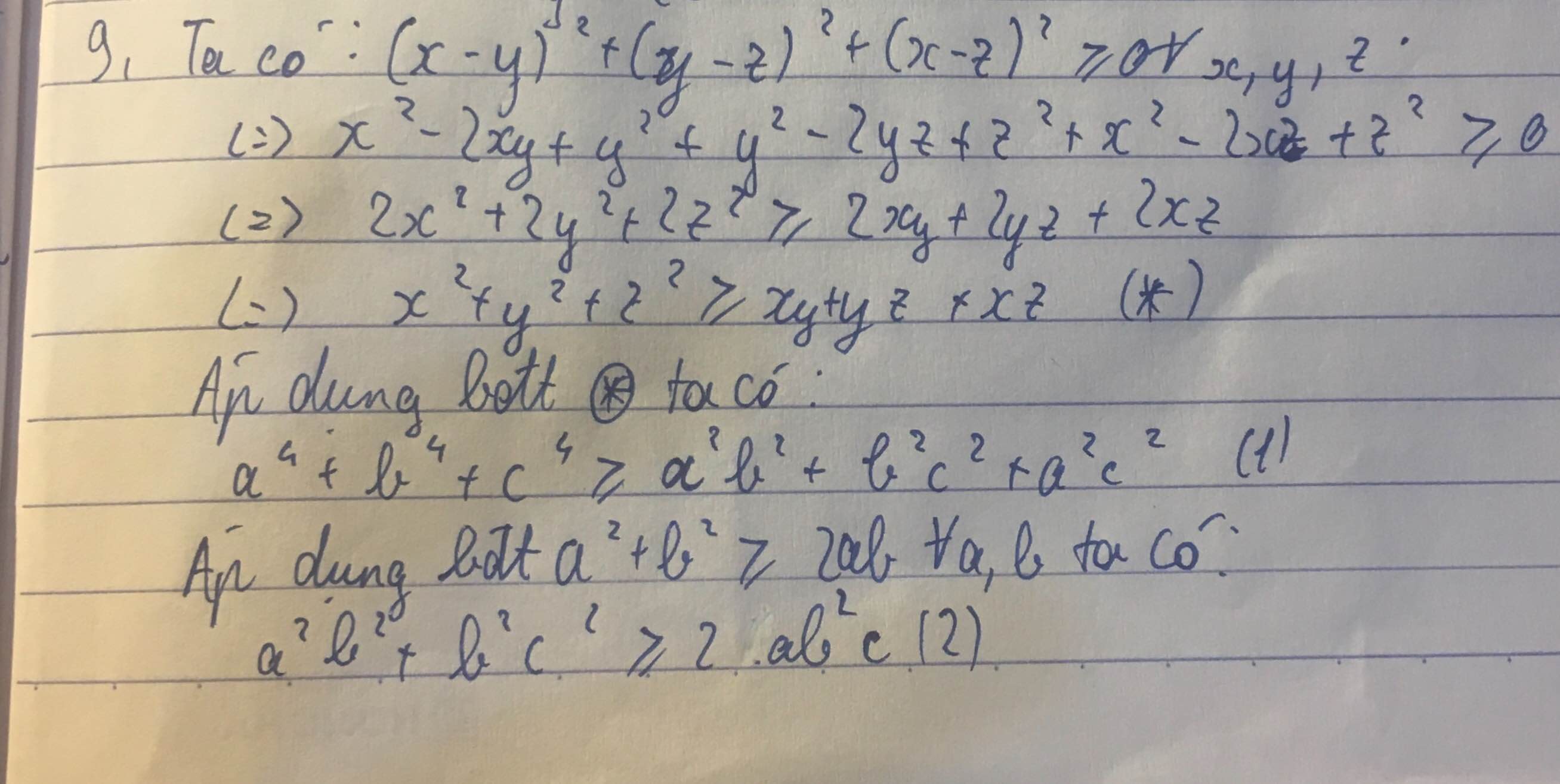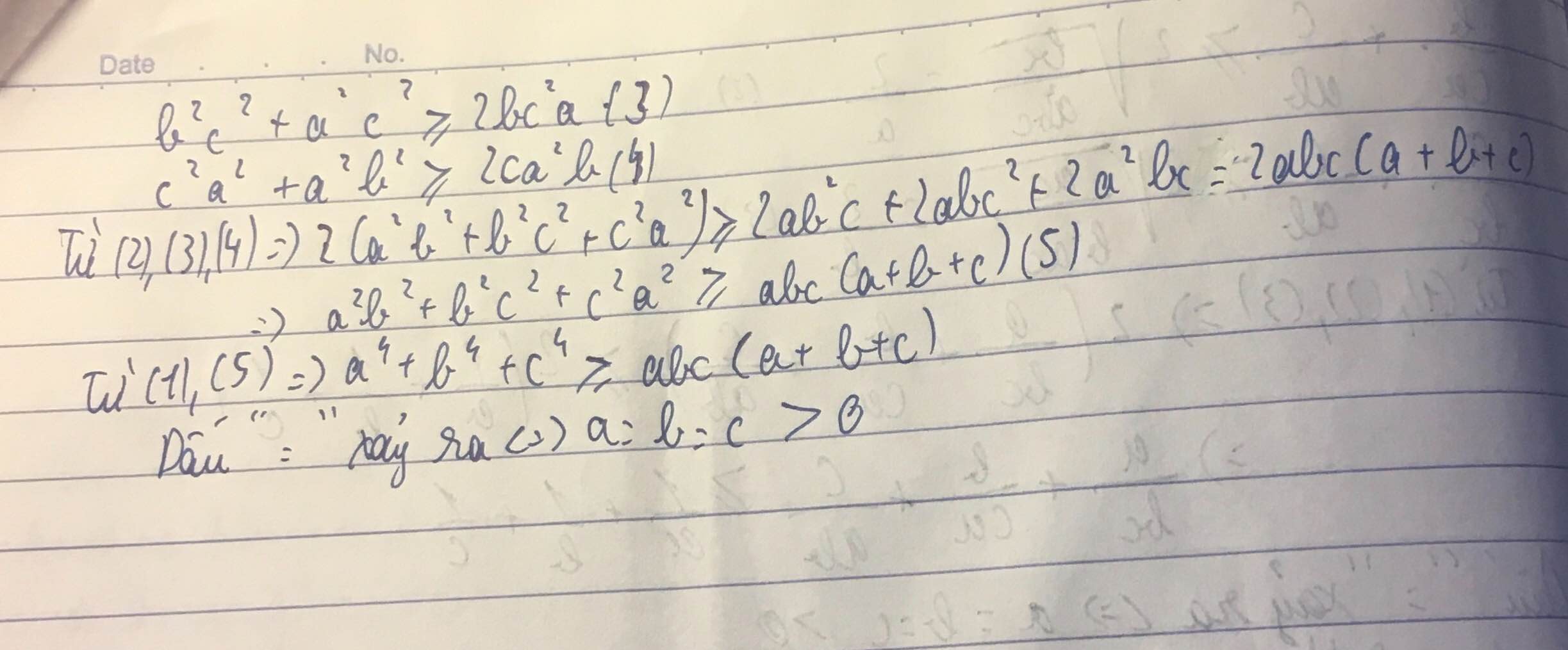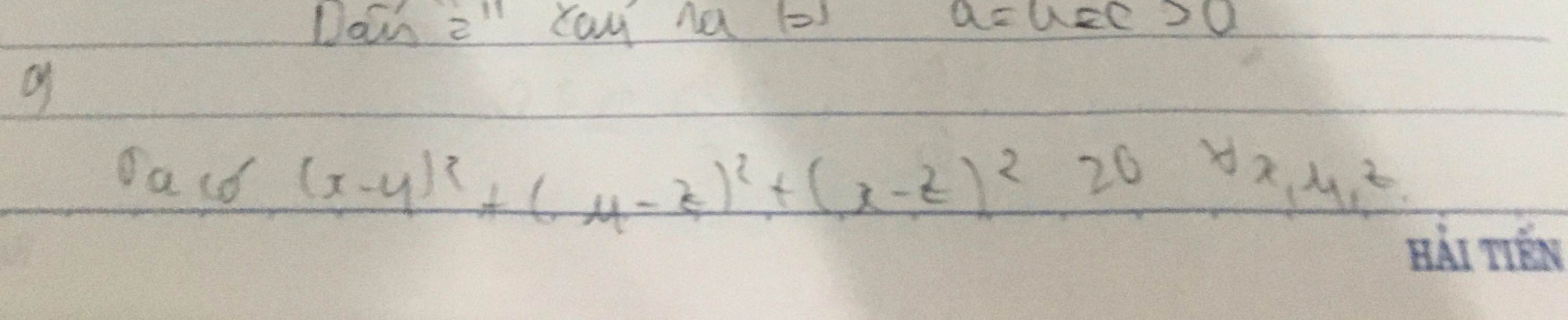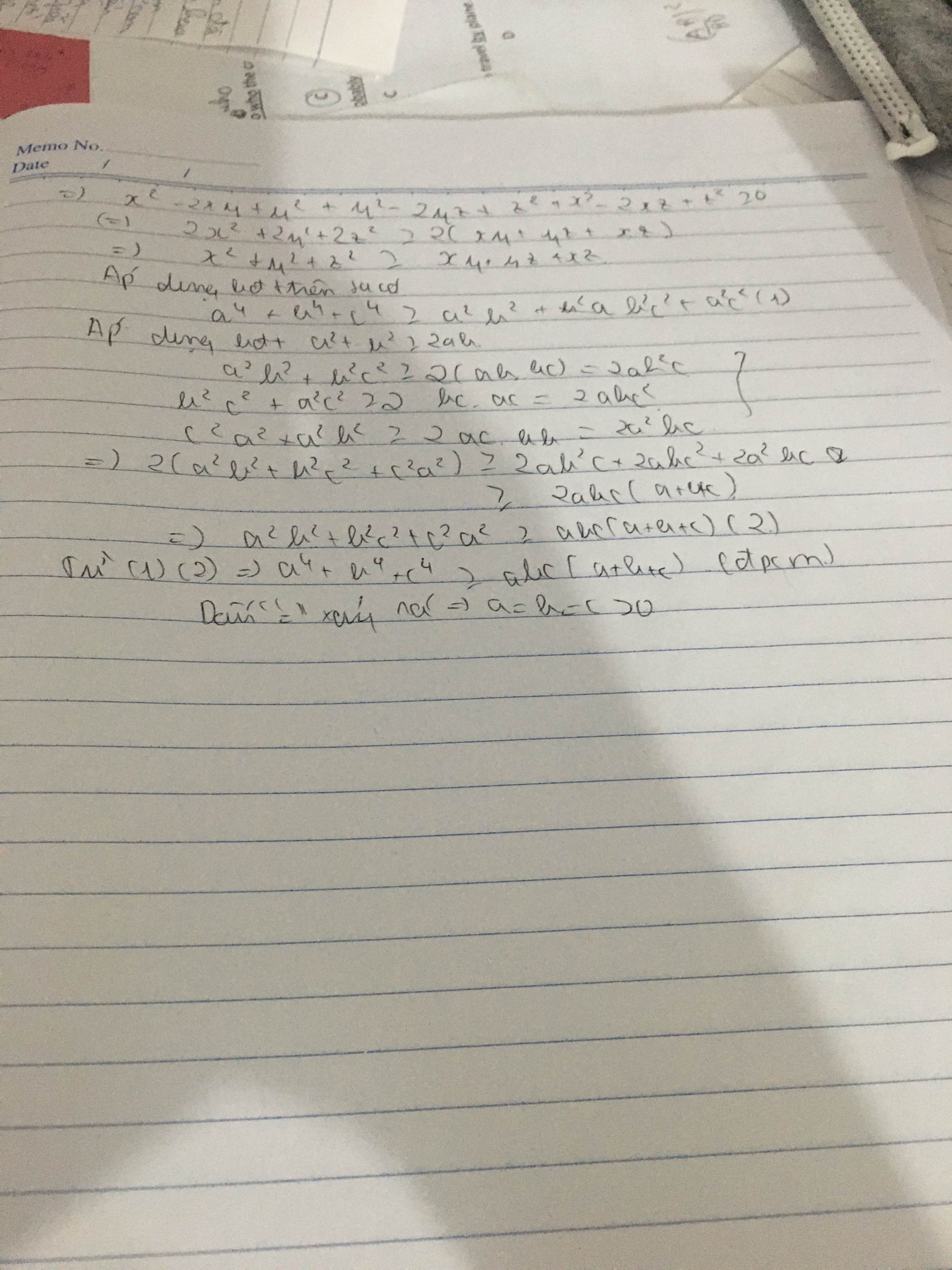Ta có : a^4 +b^4 +c^4 ≥ a^2b^2 + b^2c^2 + c^2a^2 (*)
Mà a^2b^2+b^2c^2 ≥ 2acb^2
b^2c^2 + c^2a^2 ≥ 2bac^2
c^2a^2+a^2b^2 ≥ bca^2
Cộng theo vế ba bất đẳng thức trên rồi chia hai vế cho 2 ta được
a^2b^2+b^2c^2+ c^2a^2 ≥ abc(a+b+c) (**)
Từ (*)(**) => đpcm
Sử dụng bất đẳng thức Cô si ta có
Từ đó .