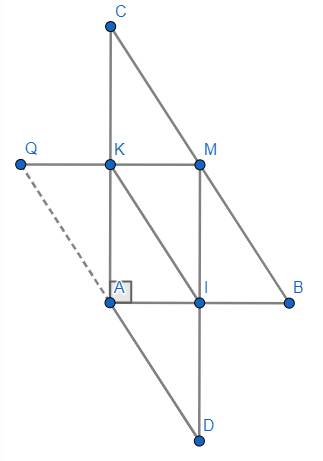
(a) \(I,M\) là trung điểm của \(AB,BC\Rightarrow IM\) là đường trung bình của \(\Delta ABC\Rightarrow\left\{{}\begin{matrix}IM\left|\right|AC\Leftrightarrow MD\left|\right|AC\left(1\right)\\IM=\dfrac{1}{2}AC\end{matrix}\right.\)
Lại có: \(IM=ID\Rightarrow MD=2IM=2\cdot\dfrac{1}{2}AC=AC\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow ADMC\) là hình bình hành (điều phải chứng minh).
(b) \(\left\{{}\begin{matrix}MI\left|\right|AC\left(cmt\right)\\AC\perp AB\left(gt\right)\end{matrix}\right.\Rightarrow MI\perp AB\Rightarrow\hat{AIM}=90^o\left(3\right)\).
\(M,K\) là trung điểm của \(BC,AC\Rightarrow MK\) là đường trung bình của \(\Delta ABC\Rightarrow MK\left|\right|AB\), mà \(AB\perp AC\left(gt\right)\Rightarrow MK\perp AC\Rightarrow\hat{AKM}=90^o\left(4\right)\).
Ta cũng có: \(\hat{A}=90^o\left(5\right)\).
Từ \(\left(3\right),\left(4\right),\left(5\right)\Rightarrow AIMK\) là hình chữ nhật (điều phải chứng minh).
(c) Do \(AIMK\) là hình chữ nhật (chứng minh trên) nên \(\left\{{}\begin{matrix}AK\left|\right|MI\Leftrightarrow AK\left|\right|ID\\AK=MI=ID\end{matrix}\right.\Rightarrow AKID\) là hình bình hành \(\Rightarrow IK\left|\right|AD\left(6\right)\).
Lại có: \(I,K\) là trung điểm của \(MD,MQ\Rightarrow IK\) là đường trung bình của \(\Delta MQD\Rightarrow IK\left|\right|QD\left(7\right)\)
Từ \(\left(6\right),\left(7\right)\Rightarrow Q,A,D\) thẳng hàng (điều phải chứng minh).