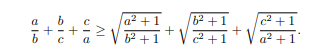BĐT bên trái: \(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\ge\sqrt{\dfrac{2a}{b+c}}+\sqrt{\dfrac{2b}{c+a}}+\sqrt{\dfrac{2c}{a+b}}\)
Ta có: \(\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)\left(ab+bc+ca\right)\ge\left(a+b+c\right)^2\)
\(\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)\left(\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\ge\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\)
Nhân vế với vế và rút gọn:
\(\Rightarrow\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)^2\ge\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)
Lại có:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{4}{a+b}+\dfrac{4}{b+c}+\dfrac{4}{c+a}\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{2}{a+b}+\dfrac{2}{b+c}+\dfrac{2}{c+a}\)
\(\Rightarrow\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)^2\ge\left(a+b+c\right)\left(\dfrac{2}{b+c}+\dfrac{2}{c+a}+\dfrac{2}{a+b}\right)\ge\left(\sqrt{\dfrac{2a}{b+c}}+\sqrt{\dfrac{2b}{c+a}}+\sqrt{\dfrac{2c}{a+b}}\right)^2\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\ge\sqrt{\dfrac{2a}{b+c}}+\sqrt{\dfrac{2b}{c+a}}+\sqrt{\dfrac{2c}{a+b}}\) (đpcm)
BĐT bên phải:
\(\sqrt{\dfrac{2a}{b+c}}+\sqrt{\dfrac{2b}{c+a}}+\sqrt{\dfrac{2c}{a+b}}\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2}\)
Ta có:
\(VT=\dfrac{2a}{\sqrt{2a.\left(b+c\right)}}+\dfrac{2b}{\sqrt{2b\left(c+a\right)}}+\dfrac{2c}{\sqrt{2c\left(a+b\right)}}\)
\(\ge\dfrac{4a}{2a+b+c}+\dfrac{4b}{2b+c+a}+\dfrac{4c}{2c+a+b}\)
\(=\dfrac{4a^2}{2a^2+ab+ac}+\dfrac{4b^2}{2b^2+bc+ab}+\dfrac{4c^2}{2c^2+ac+bc}\)
\(\ge\dfrac{4\left(a+b+c\right)^2}{2a^2+2b^2+2c^2+2\left(ab+bc+ca\right)}\ge\dfrac{4\left(a+b+c\right)^2}{2a^2+2b^2+2c^2+2\left(a^2+b^2+c^2\right)}\)
\(=\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2}\) (đpcm)