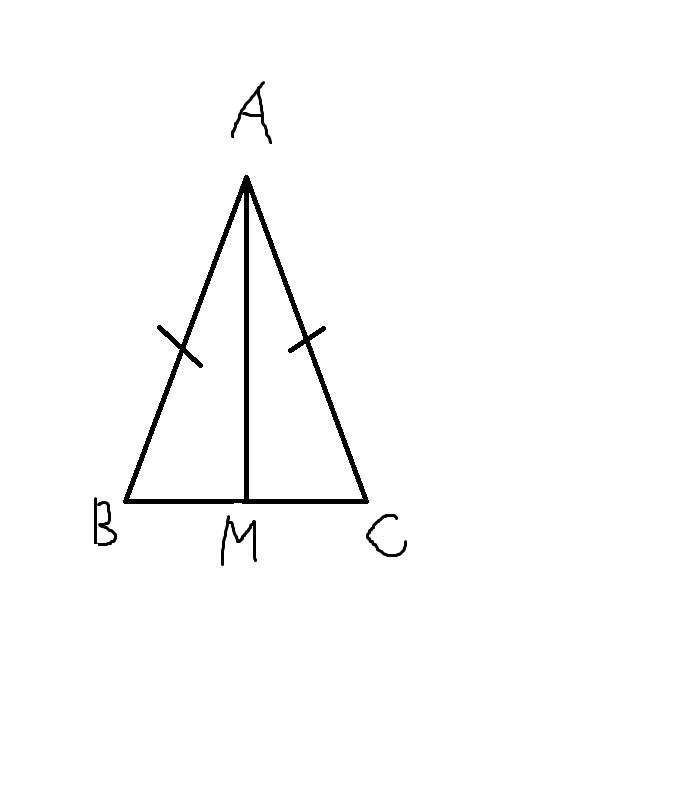Question

Cho △ABC có AB = AC, phân giác AM (M ∈ BC).
Chứng minh:
a) △ABM = △ACM
b) M là trung điểm của BC và AM ⊥ BC
@Có vẽ hình@

Answer 1

a, Vì \(\left\{{}\begin{matrix}\widehat{MAB}=\widehat{MAC}\\AB=AC\\AM.chung\end{matrix}\right.\) nên \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)

b, Vì \(\Delta ABM=\Delta ACM\) nên \(\left\{{}\begin{matrix}\widehat{AMB}=\widehat{AMC}\\BM=MC\end{matrix}\right.\)

Mà \(\widehat{AMB}+\widehat{AMC}=180^0\Rightarrow\widehat{AMB}=\widehat{AMC}=90^0\)

Vậy \(AM\perp BC\) và M là trung điểm BC