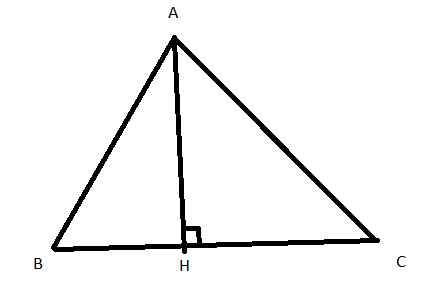
Kẻ đường cao AH của tam giác ABC
\(sinC=\dfrac{AH}{AC}\)
\(sinB=\dfrac{AH}{AB}\)
\(\Rightarrow\dfrac{sinB}{sinC}=\dfrac{\dfrac{AH}{AB}}{\dfrac{AH}{AC}}=\dfrac{AC}{AB}=\dfrac{b}{c}\Rightarrow\dfrac{b}{sinB}=\dfrac{c}{sinC}\left(1\right)\)
Kẻ đường cao CE của tam giác ABC rồi CMTT ta được:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}\left(2\right)\)
Từ (1) và (2) suy ra đpcm
Đúng 1
Bình luận (0)