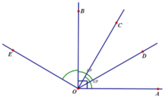
a) Vì tia OD nằm trong A O B ^ nên tia OD nằm giữa hai tia OA và OB do đó
A O D ^ + B O D ^ = A O B ^
Suy ra: A O D ^ = A O B ^ − B O D ^ = 90 0 − 60 0 = 30 0
Tương tự ta cũng có C O B ^ = 30 0 , D O C ^ = 30 0 .
b) Vì là tia phân giác của D O E ^ nên D O B ^ = B O E ^ = 60 0 .
Vì OB nằm giữa hai tia OC và OE và C O B ^ = 30 0 nên ta có
E O C ^ = E O B ^ + B O C ^ = 60 0 + 30 0 = 90 0
Vậy O C ⊥ O E
Cho AOB = 90o .Trong góc AOB vẽ các tia OC,OD sao cho: AOC=BOD=60o
a. Tính các số đo các góc AOD, DOC, COB
b. Trên nửa mặt phẳng có bờ là đường thẳng OA vẽ tia OE sao cho OB là phân giác của DOE
CMR : OC vuông góc với OE
oBài 1: Trên đg thẳng AA' lấy điểm O. Trên một nửa mặt phẳng bờ AA' vẽ tia OB sao cho góc AOB = 45o, trên nửa mặt phẳng còn lại vẽ tia OC sao cho góc AOC = 90o.
a) Gọi OB' là tia phân giác của góc A'OC. Chứng tỏ rằng hai góc AOB và A'OB' là hai góc đối đỉnh
b) Trên nửa mặt phẳng bờ AA' có chứa tia OB vẽ tia OD sao cho góc DOB = 90o. Tính số đo của góc A'OD
Trên đường thẳng AA' lấy điểm O. Trên nử mặt phẳng có bờ là AA' vẽ tia OB sao cho AOB = 450. Trên nử mặt phẳng còn lại vẽ tia OC sao cho AOC = 900. Gọi OB là tia phân giác AOC.
a) Chứng tỏ AOB và A'OB là 2 góc đối đỉnh.
b) Trên nửa mặt phẳng có bờ là ACO' chứa tia OB vẽ tia OD sao cho DOB = 900. Tính A'OD.
Mong các bn giúp mk~~ cám ơn các bn nhìu^^
Bài 4: CMR 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
Bài 5 : Cho góc AOB=90o , 2 tia OC,OD ở trong 2 góc đó sao cho góc AOC = góc BOD = 60o Trên nửa mặt phẳng bờ OA có chứa tia OB vẽ OE sao cho OB là phân giác của góc DOE
a, 2 tia OC,OD là phân giác của góc nào ? Vì sao ?
b, Có nhận xét gì về 2 tia OC,OE
Trên đường thẳng AM lấy điểm O nằm giữa A và M. Trên cùng nửa mặt phẳng bờ là đường thẳng AM vẽ các tia OB và OC sao cho góc MOC bằng 115 độ; góc BOc bằng 70 độ. Trên nửa mặt phẳng đối diện dựng tia OD (D không cùng nằm trên nửa mặt phẳng với B và C bờ là AM) sao cho góc AOD bằng 45 độ. a) Tia OB có nằm giữa hai tia OM, OC không? vì sao? b) Tính góc MOB và góc AOC? c) Chứng tỏ rằng ba điểm D,O,B thẳng hàng.
Cho xoy = 90 .Trong góc xoy vẽ các tia OC,OD sao cho: AOC = BOD = 60 độ.
a. Tính các số đo các góc AOD = DOC = COB;
b. Trên nửa mặt phẳng có bờ là đường thẳng OA và chứa tia OE sao cho OB là phân giác của DOE. Chứng minh rằng: OC ⊥ OE
Cho xoy = 90 .Trong góc xoy vẽ các tia OC,OD sao cho: AOC = BOD = 60 độ.
a. Tính các số đo các góc AOD ,DOC ,COB;
b. Trên nửa mặt phẳng có bờ là đường thẳng OA và chứa tia OE sao cho OB là phân giác của DOE. Chứng minh rằng: OC ⊥ OE
Cho xoy = 90 .Trong góc xoy vẽ các tia OC,OD sao cho: AOC = BOD = 60 độ.
a. Tính các số đo các góc AOD = DOC = COB;
b. Trên nửa mặt phẳng có bờ là đường thẳng OA và chứa tia OE sao cho OB là phân giác của DOE.
Chứng minh rằng: Oe ⊥ Oc
Cho xoy = 90 .Trong góc xoy vẽ các tia OC,OD sao cho: AOC = BOD = 60 độ.
a. Tính các số đo các góc AOD ,DOC ,COB;
b. Trên nửa mặt phẳng có bờ là đường thẳng OA và chứa tia OE sao cho OB là phân giác của DOE. Chứng minh rằng: OC ⊥ OE
