Chọn đáp án A
Do z 2 ≠ 0 nên chia cả hai vế của z 1 2 + z 2 2 = z 1 z 2 cho z 2 2 , ta được:
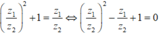
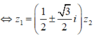
![]()
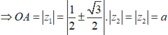
Ta có A B = z 1 - z 2 = a
Vậy OA = OB = AB hay tam giác OAB đều.
Chọn đáp án A
Do z 2 ≠ 0 nên chia cả hai vế của z 1 2 + z 2 2 = z 1 z 2 cho z 2 2 , ta được:
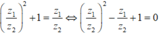
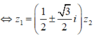
![]()
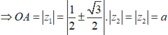
Ta có A B = z 1 - z 2 = a
Vậy OA = OB = AB hay tam giác OAB đều.
Cho hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự z 0 , z 1 khác 0 và thỏa mãn đẳng thức z 0 2 + z 1 2 = z 0 z 1 . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ)? Chọn phương án đúng và đầy đủ nhất.
A. Cân tại O.
B. Vuông cân tại O.
C. Đều.
D. Vuông tại O.
Cho hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự z 1 , z 2 khác 0 và thỏa mãn đẳng thức z 1 2 + z 2 2 = z 1 z 2 . . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ). Chọn phương án đúng và đầy đủ nhất
A. Vuông cân tại O
B. Cân tại O
C. Đều
D. Vuông tại O
Giả sử m = - a b , a , b ∈ Z + , ( a , b ) = 1 là giá trị thực của tham số m để đường thẳng d : y = - 3 x + m cắt đồ thị hàm số y = 2 a + 1 x - 1 tại hai điểm phân biệt A,B sao cho trọng tâm tam giác OAB thuộc đường thẳng ∆ : x - 2 y - 2 = 0 với O là gốc tọa độ. Tính a+2b
A. 2
B. 5
C. 11
D. 21
Cho số phức z = a + b i , a , b ∈ R . Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc hình tròn tâm O bán kính R = 2 như hình vẽ bên thì điều kiện của a và b là
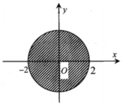
A. - 2 ≤ a ≤ 2 - 2 ≤ b ≤ 2
B. a 2 + b 2 ≤ 4
C. a 2 + b 2 > 4
D. a < - 2 ; b > 2
Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1 - 3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.
A. M(3;1)
B. M(3;-1)
C. M(1;3)
D. M(1;-3)
Cho M,N là 2 điểm trong mặt phẳng phức biểu diễn số phức z, w khác 0 thỏa mãn z 2 + w 2 = z w . Hỏi tam giác OMN là tam giác gì?
A. Đều
B. Vuông
C. Cân
D. Thường
Cho số phức z thỏa mãn: z − 1 + i = 2 . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
A. Một đường thẳng
B. Một đường Parabol
C. Một đường tròn có bán kính bằng 2
D. Một đường tròn có bán kính bằng 4
Cho z 1 = 2 + i , z 2 = - 2 + i , z 3 = z + b i với b > 0 thỏa mãn các điểm biểu diễn hình học của z 1 , z 2 , z 3 tạo thành tam giác đều. Khẳng định nào sau đây đúng?
A . a + b = 2 3 + 1
B . a - b = 2 3 - 1
C . 2 a + b = 2 3
D . a + b = - 2 3
Gọi m là số thực dương sao cho đường thẳng y = m + 1 cắt đồ thị hàm số y = x 4 − 3 x 2 − 2 tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng?
A. m ∈ 7 9 ; 9 4
B. m ∈ 1 2 ; 3 4
C. m ∈ 3 4 ; 5 4
D. m ∈ 5 4 ; 7 4