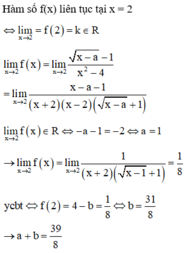Các câu hỏi tương tự
Cho hàm số
f
(
x
)
a
x
+
b
c
x
+
d
với a,b,c,d là các số thực và c
≠
0. Biết f(1)1, f(2)2 và f(f(x))x với mọi
x
≠
-
d
c
. Tính
l
i
m...
Đọc tiếp
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Cho hàm số yf(x) có đạo hàm liên tục trên
−
1
;
2
. Đồ thị của hàm số yf(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là
5
12
và
8
3
.
Biết
f
−
1
19
12...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên − 1 ; 2 . Đồ thị của hàm số y=f'(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f − 1 = 19 12 , tính f(2).
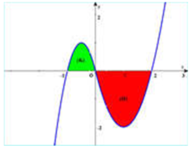
A. f 2 = 23 6 .
B. f 2 = − 2 3 .
C. f 2 = 2 3 .
D. f 2 = 11 6 .
Cho hàm số y f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y f(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là
5
12
và
8
3
. Biết
f
-
1
19
12
, tính f(2) A.
f
2
-
2
3...
Đọc tiếp
Cho hàm số y =f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y = f'(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f - 1 = 19 12 , tính f(2)
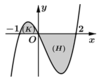
A. f 2 = - 2 3
B. f 2 = 2 3
C. f 2 = 11 6
D. f 2 = 3
Đường thẳng x k cắt đồ thị hàm số
y
log
5
x
và đồ thị hàm số
y
log
3
(
x
+
4
)
. Khoảng cách giữa các giao điểm là 1/2. Biết
k
a
+
b
,
trong đó a, b là các số nguyên. Khi đó tổng a + b bằng A. 7 B. 6 C. 8 D. 5
Đọc tiếp
Đường thẳng x = k cắt đồ thị hàm số y = log 5 x và đồ thị hàm số y = log 3 ( x + 4 ) . Khoảng cách giữa các giao điểm là 1/2. Biết k = a + b , trong đó a, b là các số nguyên. Khi đó tổng a + b bằng
A. 7
B. 6
C. 8
D. 5
Cho a, b là các số thực và hàm số
f
x
x
−
a
−
1
x
2
−
4...
Đọc tiếp
Cho a, b là các số thực và hàm số f x = x − a − 1 x 2 − 4 k h i x ≠ 2 2 x − b k h i x = 2 liên tục tại x = 2. Tính giá trị của biểu thức T=a+b.
A. T = 31 8
B. T = 5
C. T = 3
D. T = 39 8
Cho hàm số y f(x), y g(x) liên tục trên [a;b] và số thực k tùy ý. Trong các phát biểu sau, phát biểu nào sai? A.
∫
a
b
f
x
d
x
-
∫
b
a
f
x
d
x
.
B.
∫
a
a...
Đọc tiếp
Cho hàm số y = f(x), y = g(x) liên tục trên [a;b] và số thực k tùy ý. Trong các phát biểu sau, phát biểu nào sai?
A. ∫ a b f x d x = - ∫ b a f x d x .
B. ∫ a a k f x d x = 0 .
C. ∫ a b f x + g x d x = ∫ a b f x d x + ∫ a b g x d x .
D. ∫ a b x f x d x = x ∫ a b f x d x .
Cho hàm số yf(x), yg(x) liên tục trên [a;b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai? A.
∫
a
a
k
f
x
d
x
0
B.
∫
a
b
x
f
x
d
x
x
∫
a
b
f
x
d...
Đọc tiếp
Cho hàm số y=f(x), y=g(x) liên tục trên [a;b] và số thực k tùy ý. Trong các khẳng định sau, khẳng định nào sai?
A. ∫ a a k f x d x = 0
B. ∫ a b x f x d x = x ∫ a b f x d x
C. ∫ a b f x + g x d x = ∫ a b f x d x + ∫ a b g x d x
D. ∫ a b f x d x = - ∫ b a f x d x
Cho hàm số
y
f
(
x
)
có đạo hàm trên
ℝ
. Xét các hàm số
g
(
x
)
f
x
−
f
2
x
và
h
(
x
)
f
(
x
)
−
f
(
4
x
)
. Biết rằng
g...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020
Cho hàm số
y
f
(
x
)
có đạo hàm trên khoảng
a
;
b
. Xét các mệnh đề sau: I. Nếu hàm số
y
f
(
x
)
đồng biến trên khoảng
a
;
b
thì
f...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1