Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho a,b,c là độ dài của 3 cạnh tam giác. Chứng minh rằng ab + bc+ ca < a2 + b2 + c2 mà
a < hoặc = 0
Cho a, b, c là ba số khác 0 thỏa mãn: ab/a+b=bc/b+c=ca/c+a ( với giả thiết các tỉ số đều có nghĩa) và a+b=c=1 tính giá trị của biểu thức A=abc(a2+b2+c2)/ab+bc+ca
Cho các số thực không âm a,b,c thỏa mãn ab + bc + ca =1. Chứng minh rằng a2 +10(b2 + c2 ) ≥ 4
Bài 4.Cho V ABC cân tại A có góc A 40 độ.Trên cạnh AB lấy điểm D,trên tia đối của tia CA lấy điểm E sao cho BD CE. Kẻ DH và EK cùng vuông góc với đường thẳng BC. (H,K thuộc BC).1) Tính góc B, gócC của tam giác ABC.2)Chứng minh DHEK.3)Gọi M là trung điểm của HK,chứng minh M là trung điểm của DE.Bài 5.Chứng minh rằng nếu a/bb/c thì a2+b2/b2+c2 a/c với b,c khác 0.
Đọc tiếp
Bài 4.Cho V ABC cân tại A có góc A =40 độ.Trên cạnh AB lấy điểm D,trên tia đối của tia CA lấy điểm E sao cho BD= CE. Kẻ DH và EK cùng vuông góc với đường thẳng BC. (H,K thuộc BC).
1) Tính góc B, gócC của tam giác ABC.
2)Chứng minh DH=EK.
3)Gọi M là trung điểm của HK,chứng minh M là trung điểm của DE.
Bài 5.Chứng minh rằng nếu a/b=b/c thì a2+b2/b2+c2= a/c với b,c khác 0.
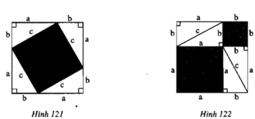
Lấy giấy trắng cắt tám tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b, gọi độ dài cạnh huyền là c. Cắt hai tấm bìa hình vuông có cạnh bằng a+b từ đó rút ra nhận xét gì về quan hệ giữa c2 và a2 + b2 ?
Đọc tiếp
Lấy giấy trắng cắt tám tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b, gọi độ dài cạnh huyền là c. Cắt hai tấm bìa hình vuông có cạnh bằng a+b
từ đó rút ra nhận xét gì về quan hệ giữa c2 và a2 + b2 ?
cho tỷ lệ thức a/c=c/b (a,b,c khác 0). Chứng minh
a) a2+c2/b2+c2=a/b
b) b2-a2 / a2+c2= b-a/a
Cho a,b,c là độ dài 3 cạnh của một tam giác
CM ab+bc+ca nhỏ hơn hoặc bằng a^2+b^2+c^2<2<ab+bc+ca>
cho x,y ,z là 3 cạnh của một tam giác
CMR: xy+xz+yz>\(\dfrac{x^2+y^2+z^2}{2}\)
Cho a,b,c là cạnh của một tam giác . CMR\(\left(ab+bc+ca\right)2>a^2+b^2+c^2\)
