với 
đồng biến trên tập 
với 
nghịch biến trên tập 
nằm phía trên trục hoành và đồ thị hàm số 
nằm phía dưới trục hoành
Các câu hỏi tương tự
Biết đồ thị hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S...
Đọc tiếp
Biết đồ thị hàm số f ( x ) = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2 .
B. S 1 S 2 = 1 4 .
C. S 1 S 2 = 1 2 .
D. S 1 S 2 = 1 .
Biết đồ thị hàm số
f
x
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S
1
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi
S
2
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm...
Đọc tiếp
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Hình phẳng giới hạn bởi đồ thị hàm số yf(x) và trục hoành gồm hai phần, phần nằm phía trên trục hoành có diện tích S1
8
3
và phần nằm phía dưới trục hoành có diện tích S2
5
12
(tham khảo hình vẽ bên). Tính
I
∫
-
1
0
f
(
3
x
+
1
)
d
x...
Đọc tiếp
Hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành gồm hai phần, phần nằm phía trên trục hoành có diện tích S1= 8 3 và phần nằm phía dưới trục hoành có diện tích S2= 5 12 (tham khảo hình vẽ bên). Tính I = ∫ - 1 0 f ( 3 x + 1 ) d x .
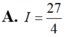
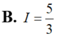
Cho hàm sốa) Xác định a để hàm số luôn đồng biến.b) Xác định a để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt.c) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với a 3/2.Từ đó suy ra đồ thị của hàm số
Đọc tiếp
Cho hàm số
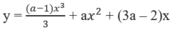
a) Xác định a để hàm số luôn đồng biến.
b) Xác định a để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với a = 3/2.
Từ đó suy ra đồ thị của hàm số
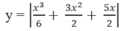
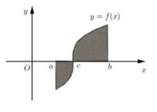
Cho hàm số y f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm a c (acb) (như hình vẽ bên). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng xa; xb Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm a = c (a<c<b) (như hình vẽ bên). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b Mệnh đề nào dưới đây đúng?
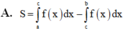
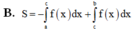
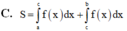
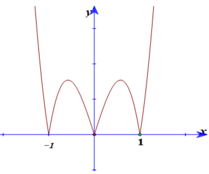
Cho hàm số y f( x) ax4+ bx2+ c ( a 0) có đồ thị (C), đồ thị hàm số y f’(x). Đồ thị hàm số y f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành? A.
7
15
B.
8
15
C.
14
15
D.
16
15
Đọc tiếp
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 7 15
B. 8 15
C. 14 15
D. 16 15
Cho hàm số y f(x) có đồ thị (C) nằm trên trục hoành. Hàm số y f(x) thỏa mãn các điều kiện
y
2
+
y
.
y
-
4
và
f
0
1
;
f...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị (C) nằm trên trục hoành. Hàm số y = f(x) thỏa mãn các điều kiện y ' 2 + y ' ' . y = - 4 và f 0 = 1 ; f 1 4 = 5 2 Diện tích hình phẳng giới hạn bởi (C) và trục hoành gần nhất với số nào dưới đây?
A. 0,95.
B. 0,96.
C. 0,98.
D. 0,97.
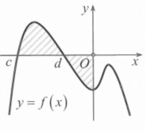
Cho hàm số f(x) liên tục trên R có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số f(x) trục hoành và trục tung. Khẳng định nào sau đây đúng:
Đọc tiếp
Cho hàm số f(x) liên tục trên R có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số f(x) trục hoành và trục tung. Khẳng định nào sau đây đúng:
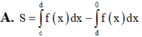
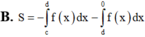
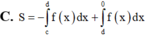
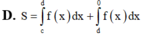
Cho hàm số
y
x
4
-
6
x
2
+
m
có đồ thị
C
m
.Giả sử
C
m
cắt trục hoành tại bốn điểm phân biệt sao cho hình phẳng giới hạn bởi
C
m
và trục hoành có phần phía trên trục hoành và phần phía dưới trục hoành có diện tích...
Đọc tiếp
Cho hàm số y = x 4 - 6 x 2 + m có đồ thị C m .Giả sử C m cắt trục hoành tại bốn điểm phân biệt sao cho hình phẳng giới hạn bởi C m và trục hoành có phần phía trên trục hoành và phần phía dưới trục hoành có diện tích bằng nhau. Khi đó m = a b (với a,b là các số nguyên, b > 0 ; a b là phân số tối giản). Giá trị của biểu thức S=a+b là:
A. 7.
B. 6.
C. 5.
D. 4.
Cho hàm số
y
x
3
-
3
x
2
+
3
mx
+
m
-
1
. Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục Ox có diện tích phần nằm phía trên trục Ox và phần nằm phía dưới trục Ox bằng nhau. Giá trị của m là A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 3 mx + m - 1 . Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục Ox có diện tích phần nằm phía trên trục Ox và phần nằm phía dưới trục Ox bằng nhau. Giá trị của m là
A. 
.
B. 
.
C. 
.
D. 
.