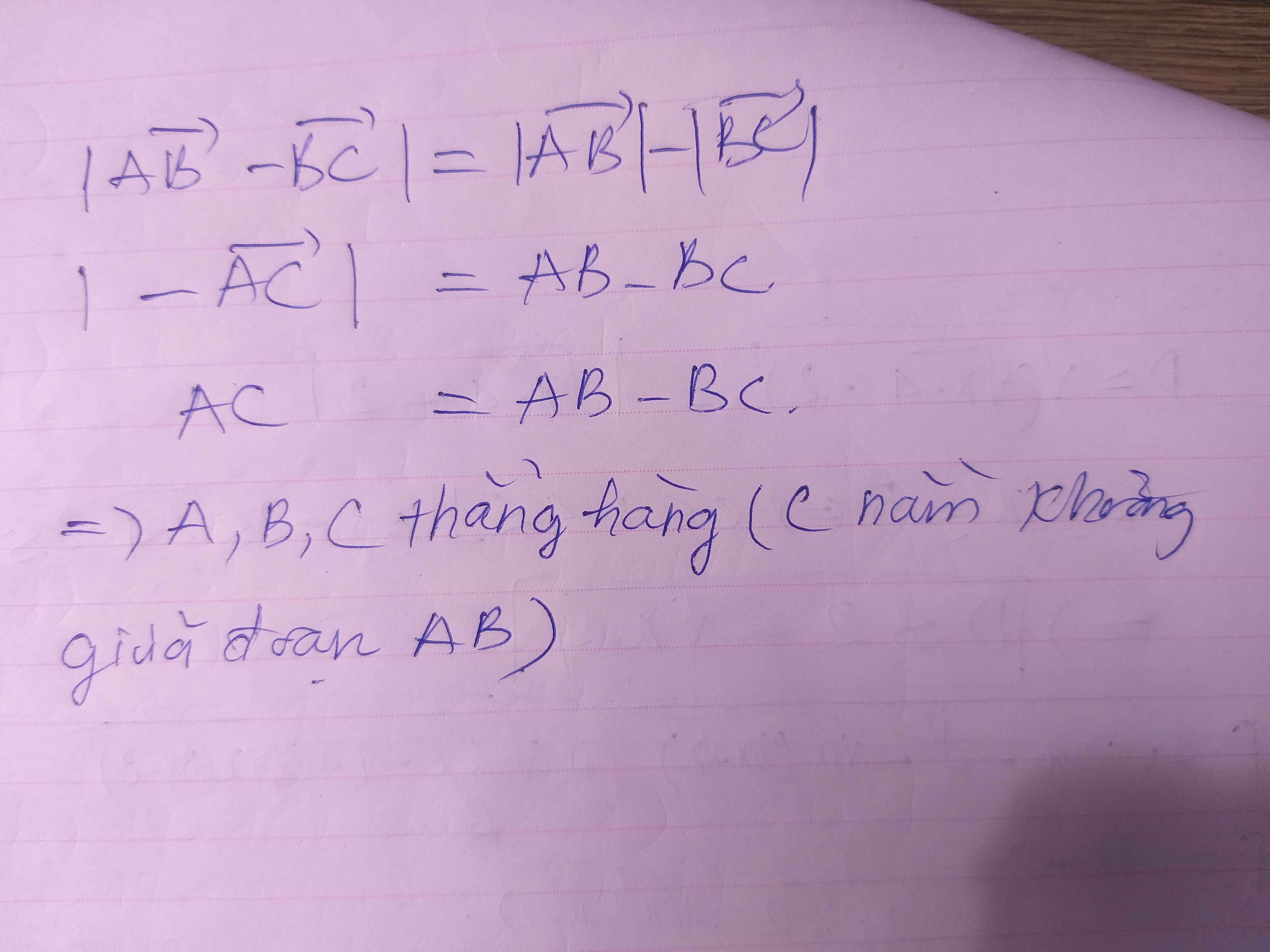Theo bất đẳng thức tam giác với các vecto \(\overrightarrow{u}và\overrightarrow{v}\)
\(\left|\overrightarrow{u}+\overrightarrow{v}\right|\ge\left|\overrightarrow{u}\right|+\left|\overrightarrow{v}\right|\)
Dấu "=" xảy ra khi vecto u và v cùng hướng ,cùng chiều
Tương tự ta có Bđt hiệu vecto:
\(\left|\overrightarrow{u}-\overrightarrow{v}\right|\ge\left|\overrightarrow{u}\right|-\left|\overrightarrow{v}\right|\)
Dấu "=" xảy ra khi 2 vecto u và v cùng phương ngược chiều
==> Để \(\left|\overrightarrow{AB}-\overrightarrow{BC}\right|=\left|\overrightarrow{AB}\right|-\left|\overrightarrow{AC}\right|\)thì \(\overrightarrow{AB}và\overrightarrow{BC}\) phải cùng phương ngược chiều
=> 3 điểm A,B,C thẳng hàng và B nằm giữa AC
ý là nếu muốn bằng thì vecto AB với vecto BC phải ngược hướng, khi ấy thì B phải nằm giữa thì sao mà AB > AC được ta