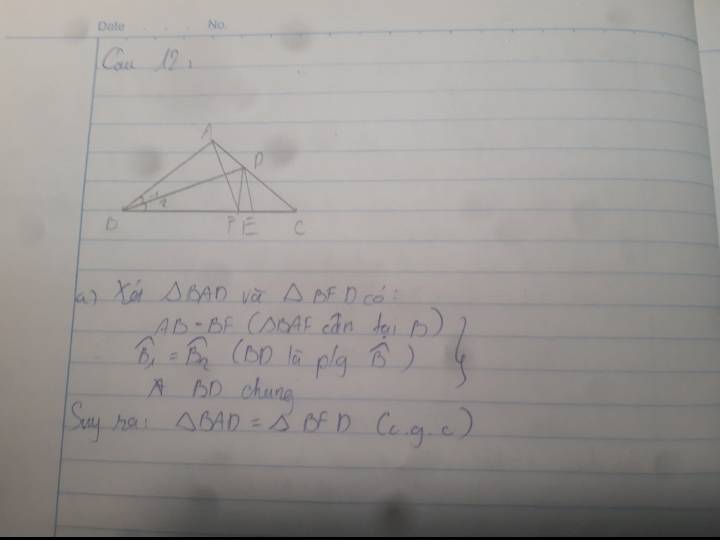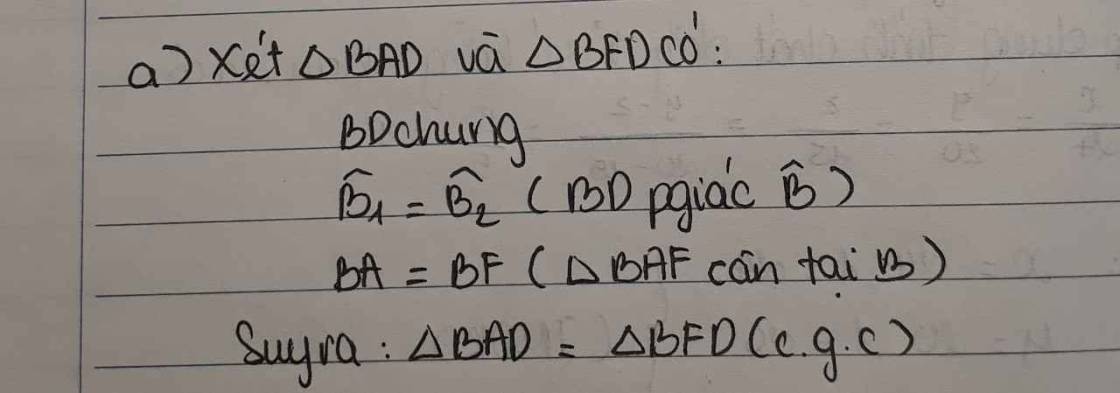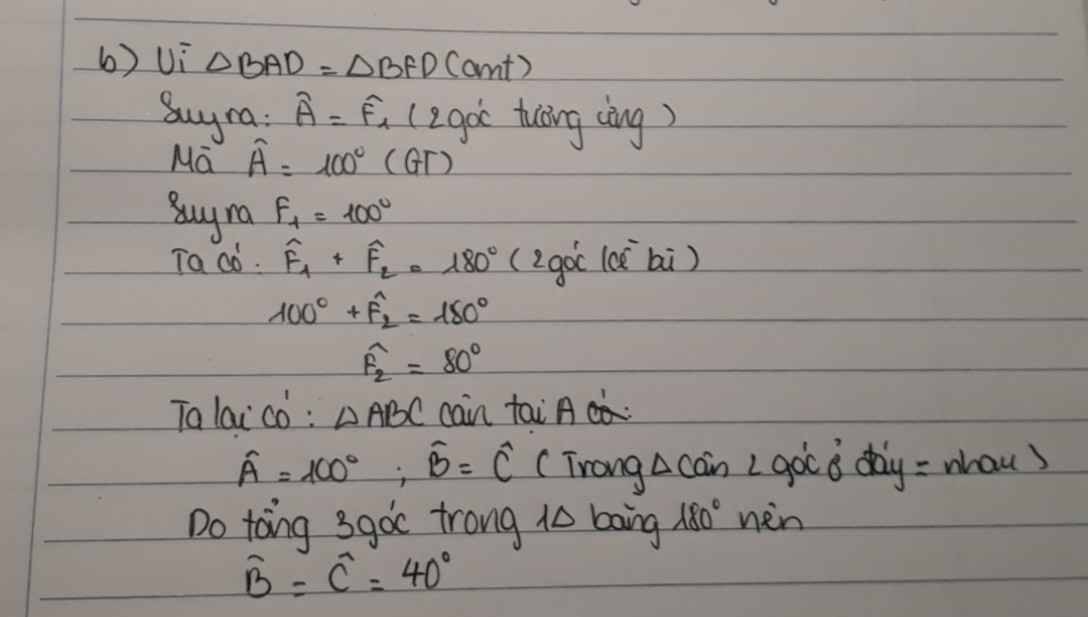Question

Câu 12. (2 điểm) Cho tam giác $ABC$ cân tại đỉnh $A$ ;$BD$ là phân giác của góc $B$. Các tam giác $BAF$ và $BDE$ cùng cân tại đỉnh $B$.

a) Chứng minh $\Delta BAD = \Delta BFD$.

b) Chứng minh $\Delta DEF$ cân.

Answer 1

a, Tam giác ABC cân tại A nên  \(\widehat{B}\) = \(\widehat{C}\)

⇒ \(\widehat{ABM}\) = \(\widehat{ACN}\) (1)

AB = AC (2)

\(\widehat{BAM}\) = \(\widehat{CAN}\) = 90⁰ (3)

Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)

b, BM = CN  ( Δ BAM =  ΔCAN)

   BM = BN + MN = MN + MC 

   ⇒ BN  = CM 

c, \(\widehat{BAN}\) + \(\widehat{NAC}\) = \(\widehat{BAC}\) =120⁰

    \(\Rightarrow\) \(\widehat{BAN}\) = 120⁰ - \(\widehat{NAC}\) = 120⁰ - 90⁰ = 30⁰

 \(\widehat{ABN}\) = (180⁰ - 120⁰) : 2  = 30⁰

⇒ \(\widehat{BAN}\) = \(\widehat{ABN}\) = 30⁰ ⇒ △ANB cân tại N 

 

 

 

Answer 2

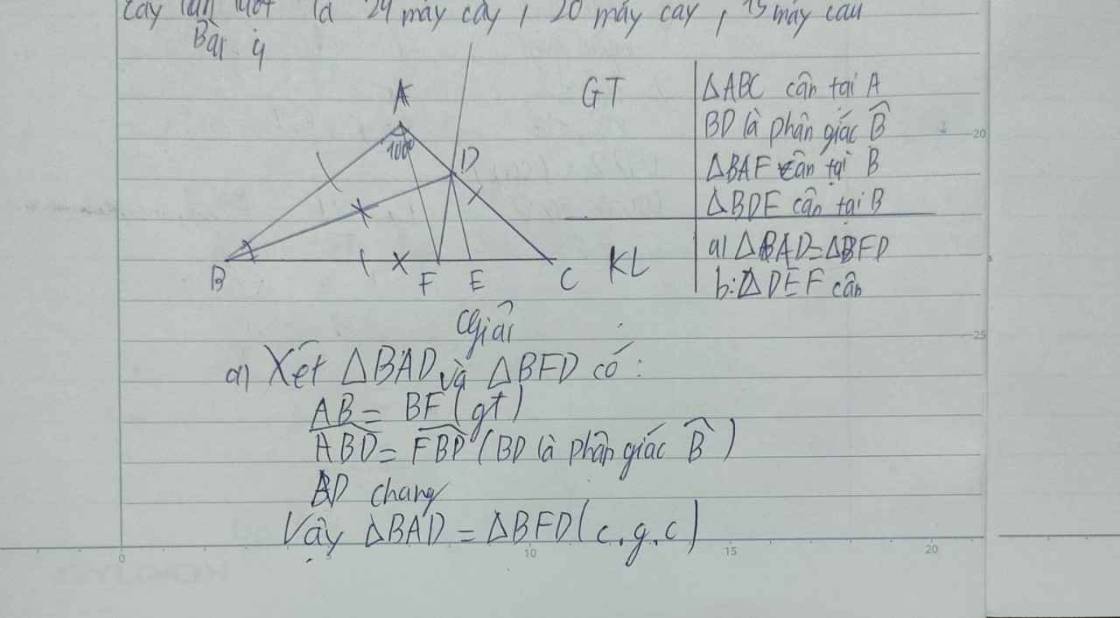
a) Xét hai tam giác $BAD$ và $BFD$ có:

     ABD^=FBD^ABD

=FBD

(vì $BD$ là tia phan giác của góc $B$);

     $AB=BF$ ($\Delta ABF$ cân tại $B$);

     $BD$ là cạnh chung;

Vậy $\Delta BAD=\Delta BFD$ (c.g.c).

b) $\Delta BAD=\Delta BFD$ suy ra BAD^=BFD^=100∘BAD

=BFD

=100∘ (hai góc tương ứng).

Suy ra DFE^=180∘−BFD^=80∘DFE

=180∘−BFD

=80∘. (1)

Tam giác $ABC$ cân tại $A$ nên B^=C^=180∘−100∘2=40∘B

=C

=2180∘−100∘​=40∘

Suy ra DBE^=20∘DBE

=20∘.

Tương tự, tam giác $BDE$ cân tại $B$ nên BED^=180∘−20∘2=80∘BED

=2180∘−20∘​=80∘. (2)

Từ (1) và (2) suy ra $\Delta DEF$ cân tại $D$.

 

Answer 3

dd

Answer 4

wsfwfw

Answer 5

wsfwfw

Answer 6

o

Answer 7

a, Tam giác ABC cân tại A nên  �^B = �^C

⇒ $\hat{}$ = $\hat{}$ (1)

AB = AC (2)

���^BAM = ���^CAN = 900 (3)

Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)

b, BM = CN  ( Δ BAM =  ΔCAN)

   BM = BN + MN = MN + MC 

   ⇒ BN  = CM 

c, ���^BAN + ���^NAC = ���^BAC =1200

    $\Rightarrow$ ���^BAN = 1200 - ���^NAC = 1200 - 900 = 300

 ���^ABN = (1800 - 1200) : 2  = 300

⇒ ���^BAN = ���^ABN = 300 ⇒ △ANB cân tại N 

Answer 8

efwaf

Answer 9

xét tam giác BAD và BFD 

bd là cạnh chung

b1=b2

ba=bf

=>đpcm

=>a=f =100

=>ad=df

b, mà bà và bde cân tại b

=>da=de

ta co da=df

da=de

=>đpcm

           

Answer 10

a, Tam giác ABC cân tại A nên  �^B = �^C

⇒ ���^ABM = ���^ACN (1)

AB = AC (2)

���^BAM = ���^CAN = 900 (3)

Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)

b, BM = CN  ( Δ BAM =  ΔCAN)

   BM = BN + MN = MN + MC 

   ⇒ BN  = CM 

c, ���^BAN + ���^NAC = ���^BAC =1200

    $\Rightarrow$ ���^BAN = 1200 - ���^NAC = 1200 - 900 = 300

 ���^ABN = (1800 - 1200) : 2  = 300

⇒ ���^BAN = ���^ABN = 300 ⇒ △ANB cân tại N 

Answer 11

    

Answer 12

Answer 13

Answer 14

Answer 15

a, Tam giác ABC cân tại A nên  �^B = �^C

⇒ ���^ABM = ���^ACN (1)

AB = AC (2)

���^BAM = ���^CAN = 900 (3)

Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)

b, BM = CN  ( Δ BAM =  ΔCAN)

   BM = BN + MN = MN + MC 

   ⇒ BN  = CM 

c, ���^BAN + ���^NAC = ���^BAC =1200

    $\Rightarrow$ ���^BAN = 1200 - ���^NAC = 1200 - 900 = 300

 ���^ABN = (1800 - 1200) : 2  = 300

⇒ ���^BAN = ���^ABN = 300 ⇒ △ANB cân tại N 

Answer 16

Answer 17

 

Answer 18

Answer 19

có tam giác baf bà cân 

xét tam giác bad = tam giác bfd có :

       ab = bf ( tam giác baf)

        ^  abd = ^dbf (  bd là phân giác)

        bd chung 

 vậy tam giác bad = tam giác bfd ( cgc)

b) có bfd = 100 độ vì ( bad = bfd)

có bfd + dfc = 180 vì kề bù

 = 100 + dfc + 180 độ

= 80 độ 

xét tam giác bde có fde là 20 vậy def sẽ là 80 

duy ra tam giác DEF cân

Answer 20

a) Xét hai tam giác ta có:

BD là cạnh chung

BA = BF (vì tam giác BAF cân)

FBD = ABD (vì BD là tia phân giác góc B)

Suy ra, BAD = BFD

Answer 21

a) Xét hai tam giác $BAD$ và $BFD$ có:

     ���^=���^ABD=FBD (vì $BD$ là tia phan giác của góc $B$);

     $AB=BF$ ($\Delta ABF$ cân tại $B$);

     $BD$ là cạnh chung;

Vậy $\Delta BAD=\Delta BFD$ (c.g.c).

b) $\Delta BAD=\Delta BFD$ suy ra ���^=���^=100∘BAD=BFD=100∘ (hai góc tương ứng).

Suy ra ���^=180∘−���^=80∘DFE=180∘−BFD=80∘. (1)

Tam giác $ABC$ cân tại $A$ nên �^=�^=180∘−100∘2=40∘B=C=2180∘−100∘​=40∘

Suy ra ���^=20∘DBE=20∘.

Tương tự, tam giác $BDE$ cân tại �

Đúng 0

Bình luận (0)

Answer 22

a, Tam giác ABC cân tại A nên  �^B = �^C

⇒ ���^ABM = ���^ACN (1)

AB = AC (2)

���^BAM = ���^CAN = 900 (3)

Kết hợp (1); (2) ; (3) ta có △BAM = △CAN (g-c-g)

b, BM = CN  ( Δ BAM =  ΔCAN)

   BM = BN + MN = MN + MC 

   ⇒ BN  = CM 

c, ���^BAN + ���^NAC = ���^BAC =1200

    $\Rightarrow$ ���^BAN = 1200 - ���^NAC = 1200 - 900 = 300

 ���^ABN = (1800 - 1200) : 2  = 300

⇒ ���^BAN = ���^ABN = 300 ⇒ △ANB cân tại N 

Answer 23

a) Xét hai tam giác BADBAD và BFDBFD có:

     ABD^ = FBD^ABD = FBD

(vì BDBD là tia phan giác của góc BB);

     AB = BF AB = BF (ΔABFΔABF cân tại BB);

     BDBD là cạnh chung;

Vậy ΔBAD = ΔBFD ΔBAD = ΔBFD (c.g.c).

b) ΔBAD = Δ BFDΔBAD = Δ BFD suy ra BAD^ = BFD^ = 100∘BAD

= BFD

= 100∘ (hai góc tương ứng).

Suy ra DFE^ = 180∘−BFD^ = 80∘DFE

=180∘ − BFD

=80∘. (1)

Tam giác ABCABC cân tại AA nên B^ = C^ =  180∘−100∘2 = 40∘B

= C

= 2180∘−100∘ ​= 40∘

Suy ra DBE^ = 20∘DBE

= 20∘.

Tương tự, tam giác BDEBDE cân tại BB nên BED^ = 180∘−20∘2 = 80∘BED

= 2180∘−20∘​ = 80∘. (2)

Từ (1) và (2) suy ra ΔDEFΔDEF cân tại D.

Answer 24

a) xét ΔBAD và ΔBFD có

BF=AB(ΔBAF cân tại B)

góc ABD= góc FBD(BD là tia phân giác)

BD chung 

 

 

Δ���=Δ���$vậy\; \Delta BAD=\Delta BFD$.( C G C)

b) 

 

���=���

$\Delta BAD=\Delta BFD$

Answer 25

xét tam giác BAD và tam giác BFD CÓ

BD chung

BF

Answer 26

ko bt

Answer 27

 $\Delta BAD=\Delta BFD$

Vì  $\Delta BADvà\Delta BFD\; là\; 2góc\; bù\; nhau$

Answer 28

Xét hai tam giác $BAD$ và $BFD$ có:

     ���^=���^ABD=FBD (vì $BD$ là tia phan giác của góc $B$);

     $AB=BF$ ($\Delta ABF$ cân tại $B$);

     $BD$ là cạnh chung;

Vậy $\Delta BAD=\Delta BFD$ (c.g.c).

b) $\Delta BAD=\Delta BFD$ suy ra ���^=���^=100∘BAD=BFD=100∘ (hai góc tương ứng).

Suy ra ���^=180∘−���^=80∘DFE=180∘−BFD=80∘. (1)

Tam giác $ABC$ cân tại $A$ nên �^=�^=180∘−100∘2=40∘B=C=2180∘−100∘​=40

 

Suy ra ���^=20∘DBE=20∘.

Tương tự, tam giác $BDE$ cân tại �

Đúng 0

Bình luận (0)

Answer 29

Xét hai tam giác $BAD$ và $BFD$ có:

     ���^=���^ABD=FBD (vì $BD$ là tia phan giác của góc $B$);

     $AB=BF$ ($\Delta ABF$ cân tại $B$);

     $BD$ là cạnh chung;

Vậy $\Delta BAD=\Delta BFD$ (c.g.c).

b) $\Delta BAD=\Delta BFD$ suy ra ���^=���^=100∘BAD=BFD=100∘ (hai góc tương ứng).

Suy ra ���^=180∘−���^=80∘DFE=180∘−BFD=80∘. (1)

Tam giác $ABC$ cân tại $A$ nên �^=�^=180∘−100∘2=40∘B=C=2180∘−100∘​=40

 

Suy ra ���^=20∘DBE=20∘.

Tương tự, tam giác $BDE$ cân tại �

Đúng 0

Bình luận (0)

Answer 30

lluluoluoilươilườilười làm