Các câu hỏi tương tự
Lập phương trình chính tắc của elip (E) biết đi qua điểm
M
3
5
;
4
5
và tam giác MF1F2 vuông tại M.
Đọc tiếp
Lập phương trình chính tắc của elip (E) biết đi qua điểm M 3 5 ; 4 5 và tam giác MF1F2 vuông tại M.




Cho elip (E) có các tiêu điểm
F
1
-
5
;
0
,
F
2
5
;
0
và một điểm M nằm trên (E) sao cho chu vi của tam giác
M
F
1
F
2
bằng 30. Khi đó phương trình chính tắc của elip là: A. ...
Đọc tiếp
Cho elip (E) có các tiêu điểm F 1 - 5 ; 0 , F 2 5 ; 0 và một điểm M nằm trên (E) sao cho chu vi của tam giác M F 1 F 2 bằng 30. Khi đó phương trình chính tắc của elip là:
A. x 2 75 + y 2 100 = 1
B. 100 x 2 + 75 y 2 = 1
C. 75 x 2 + 100 y 2 = 1
D. x 2 100 + y 2 75 = 1
Viết phương trình chính tắc của hypebol (H). Biết (H) đi qua M ( căn(2); 2căn(2) ) và N ( -1; -căn(3) )
Phương trình chính tắc của elip đi qua điểm (5;0) và có tiêu cự bằng 2 căn 5
Cho Elip có các tiêu điểm F1(-4;0) và F2(4;0) và một điểm M nằm trên (E) biết rằng chu vi của tam giác MF1F2 bằng 18. Lúc đó tâm sai của (E) là:
Đọc tiếp
Cho Elip có các tiêu điểm F1(-4;0) và F2(4;0) và một điểm M nằm trên (E) biết rằng chu vi của tam giác MF1F2 bằng 18. Lúc đó tâm sai của (E) là:
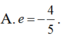
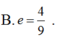
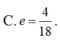
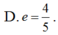
Lập phương trình chính tắc của elip trong trường hợp sau: Elip đi qua các điểm M(0; 3) và N(3; -12/5)
Lập phương trình thanh số, phương trình tổng quát của đường thẳng Δ biết: d. Δ đi qua D(2; 5) và E(3; 1)
e. Δ đi qua G(2; 5) và song song với đường thẳng d: 2x-3y-3 = 0
g. Δ đi qua H(2; 5) và vuông góc với đường thẳng d: x + 3y + 2 = 0
Trong mặt phẳng với hệ trục tọa độ $Oxy$, viết phương trình chính tắc của elip $left( E right)$ biết:
a) $left( E right)$ đi qua điểm $Mleft( dfrac{3}{sqrt{5}},;,dfrac{4}{sqrt{5}} right)$ và $M$ nhìn hai tiêu điểm ${{F}_{1}}$, ${{F}_2}$ dưới một góc vuông.
b) $left( E right)$ có độ dài trục lớn bằng $4sqrt2$, các đỉnh trên trục nhỏ và các tiêu điểm của $left( E right)$ cùng nằm trên một đường tròn.
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ $Oxy$, viết phương trình chính tắc của elip $\left( E \right)$ biết:
a) $\left( E \right)$ đi qua điểm $M\left( \dfrac{3}{\sqrt{5}}\,;\,\dfrac{4}{\sqrt{5}} \right)$ và $M$ nhìn hai tiêu điểm ${{F}_{1}}$, ${{F}_2}$ dưới một góc vuông.
b) $\left( E \right)$ có độ dài trục lớn bằng $4\sqrt2$, các đỉnh trên trục nhỏ và các tiêu điểm của $\left( E \right)$ cùng nằm trên một đường tròn.
Câu 1: Cho tam giác đều ABC có cạnh là 10a, M là trung điểm của BC. Tính | vec AB + vec AM | ? vec AM . vec BA ? Câu 2: Cho tam giác ABC vuông tại A có AB = 2a căn 3 ; AC = 2a . Tính ? vec AB . vec BC ; | vec AB - vec AC |
