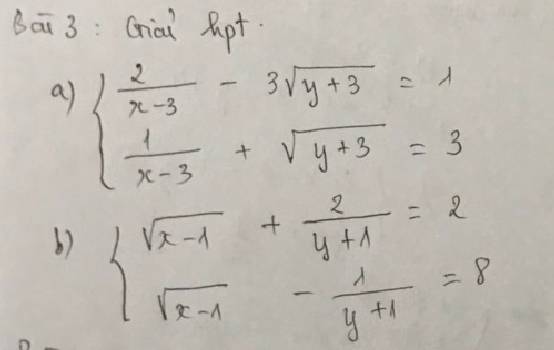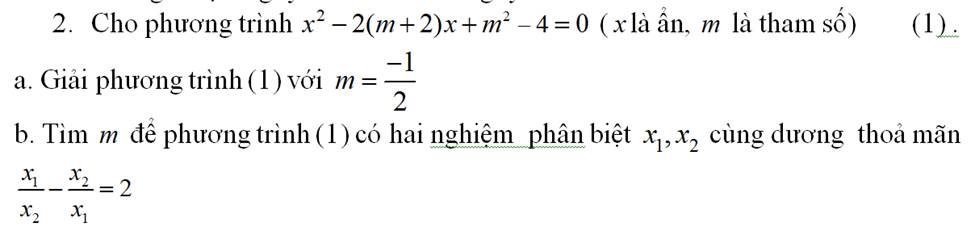\(a,\left\{{}\begin{matrix}\dfrac{2}{x-3}-3\sqrt{y+3}=1\\\dfrac{1}{x-3}+\sqrt{y+3}=3\end{matrix}\right.\)
Đặt \(a=\dfrac{1}{x-3};b=\sqrt{y+3}\left(1\right)\)
Hệ pt trở thành : \(\left\{{}\begin{matrix}2a-3b=1\\a+b=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
Thay \(a=2,b=1\) vào \(\left(1\right)\) ta có :
\(\dfrac{1}{x-3}=2\left(dk:x\ne3\right)\Leftrightarrow x-3=\dfrac{1}{2}\Leftrightarrow x=\dfrac{7}{2}\left(tm\right)\)
\(\sqrt{y+3}=1\left(dk:y\ge-3\right)\Leftrightarrow\left|y+3\right|=1\Leftrightarrow y+3=1\Leftrightarrow y=-2\left(tm\right)\)
Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(\dfrac{7}{2};-2\right)\)
\(b,\left\{{}\begin{matrix}\sqrt{x-1}+\dfrac{2}{y+1}=2\\\sqrt{x-1}-\dfrac{1}{y+1}=8\end{matrix}\right.\)
Đặt \(\sqrt{x-1}=a;\dfrac{1}{y+1}=b\left(2\right)\)
Hệ pt trở thành : \(\left\{{}\begin{matrix}a+2b=2\\a-b=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=-2\end{matrix}\right.\)
Thay \(a=6,b=-2\) vào \(\left(2\right)\) ta có :
\(\sqrt{x-1}=6\left(dk:x\ge1\right)\Leftrightarrow\left|x-1\right|=36\Leftrightarrow x-1=36\Leftrightarrow37\left(tm\right)\)
\(\dfrac{1}{y+1}=-2\left(dk:y\ne-1\right)\Leftrightarrow y+1=-\dfrac{1}{2}\Leftrightarrow y=-\dfrac{3}{2}\left(tm\right)\)
Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(37;-\dfrac{3}{2}\right)\)