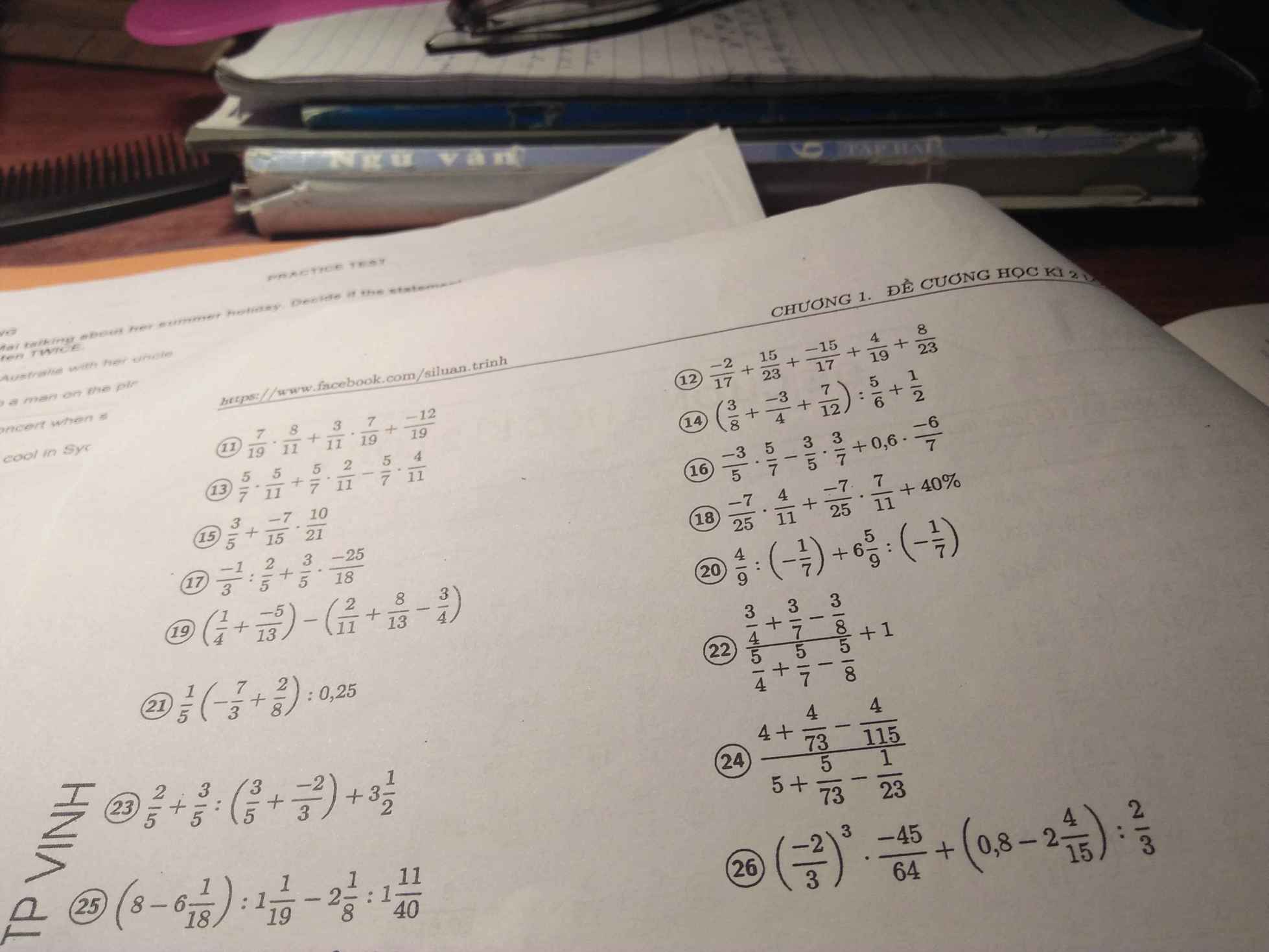Bài 6:
$\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{1}{x(x+1):2}=\frac{2022}{2023}$
$\Rightarrow \frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{x(x+1)}=\frac{4044}{2023}$
$\Rightarrow \frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+....+\frac{1}{x(x+1)}=\frac{4044}{2023}$
$\Rightarrow \frac{3-2}{2.3}+\frac{4-3}{3.4}+\frac{5-4}{4.5}+....+\frac{(x+1)-x}{x(x+1)}=\frac{4044}{2023}$
$\Rightarrow \frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{4044}{2023}$
$\Rightarrow \frac{1}{2}-\frac{1}{x+1}=\frac{4044}{2023}$
$\Rightarrow \frac{1}{x+1}=\frac{1}{2}-\frac{4044}{2023}\approx -1,5$
$\Rightarrow x+1=\frac{-2}{3}$
$\Rightarrow x=\frac{-5}{3}$
Bài 4:
$A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+....+\frac{1}{2^{2023}}$
$2A=2+1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^{2022}}$
$\Rightarrow 2A-A=2-\frac{1}{2^{2023}}$
$\Rightarrow A=2-\frac{1}{2^{2023}}$
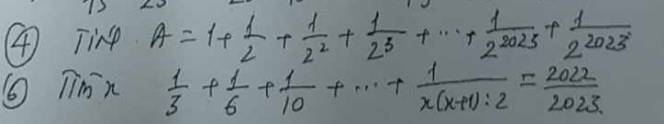



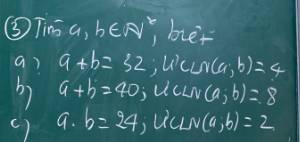

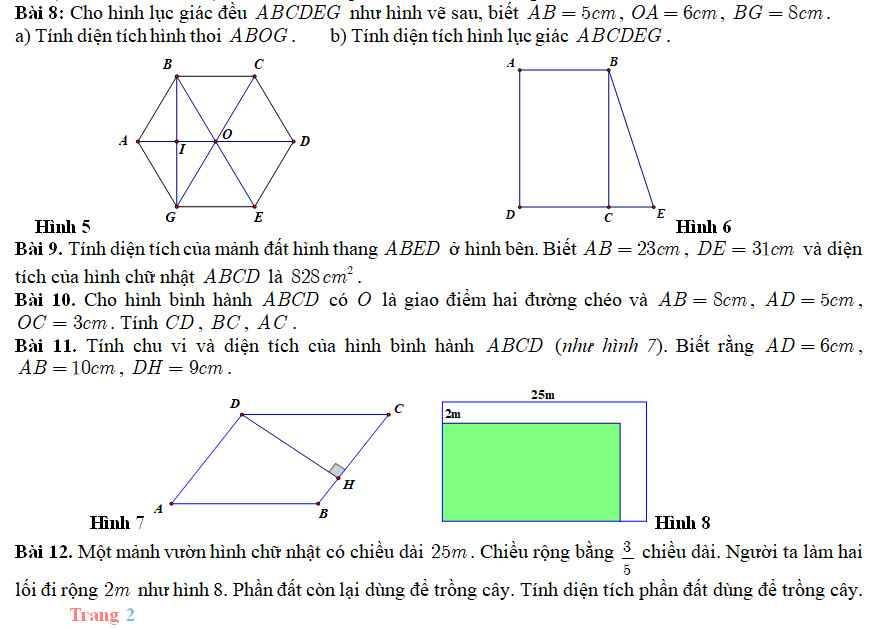 chỉ giúp em mấy bài này với ạ em đng cần gấp ạ
chỉ giúp em mấy bài này với ạ em đng cần gấp ạ