Hình 2.70a biểu diễn hình bình hành
Hình 2.70b biểu diễn hình vuông
Hình 2.70c biểu diễn hình thoi
Hình 2.70d biểu diễn hình chữ nhật
Cho hình hộp ABCD.EFGH . Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành BCGF. Trong các khẳng định sau, khẳng định nào đúng?
A. B D → , A K → , G F → đồng phẳng
B. B D → , I K → , G F → đồng phẳng
C. B D → , E K → , G F → đồng phẳng
D. B D → , I K → , G C → đồng phẳng
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên
2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên
3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là
4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên
5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên
6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhất
A. ba điểm phân biệt
B. 1 điểm và 1 đường thẳng
C. 2 đường thẳng cắt nhau
D. 4 điểm phân biệt
Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biểu nào sau đây là đúng?
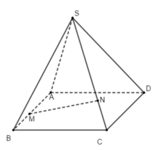
A. Giao điểm của MN với (SBD) là giao điểm của MN với BD.
B. Đường thẳng MN không cắt mặt phẳng (SBD)
C. Giao điểm của MN với (SBD) là giao điểm của MN với SI, trong đó I là giao điểm của CM với BD
D. Giao điểm của MN với (SBD) là M.
Hình chiếu song song của một hình vuông có thể là hình bình hành được không?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN//BS, NP//CD, MQ // CD. Những khẳng định nào sau đây là đúng?
1) PQ // SA
(2) PQ // MN
(3) tứ giác MNPQ là hình thang
(4) tứ giác MNPQ là hình bình hành
A. (4)
B. (1) và (3)
C. (2) và (3)
D. (2) và (4)
Trong các hình tam giác đều, hình bình hành, ngũ giác đều, lục giác đều, hình nào có tâm, đối xứng?
Cho hình lăng trụ ABC.A'B'C' có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng (ABB'A') là tâm của hình bình hành ABB'A'. Thể tích khối lăng trụ ABC.A'B'C' tính theo a là:
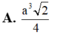
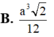
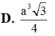
Trên mặt phẳng (α) cho hình bình hành A 1 B 1 C 1 D 1 . Về một phía đối với mặt phẳng (α) ta dựng hình bình hành A 2 B 2 C 2 D 2 . Trên các đoạn A 1 A 2 , B 1 B 2 , C 1 C 2 , D 1 D 2 ta lần lượt lấy các điểm A, B, C, D sao cho
A A 1 A A 2 = B B 1 B B 2 = C C 1 C C 2 = D D 1 D D 2 = 3
Chứng minh rằng tứ giác ABCD là hình bình hành
