Mình nghĩ bạn nên dùng web Wolfram|Alpha: Computational Intelligence để phân !
Máy mình window XP quá lỗi thời nên không làm được nha bạn ~
Bạn nhập là:factor 2x^4+3x^3+2x^2+3 là ok nhé !
=2x^2(x^2+1)+3(x^3+1)
=2x^2(x^2+2x+1)+(3x-3)(x^2+2x+1)
=(x^2+2x+1)(2x^2+3x-3)
a. 1,2 – (x – 0,8) = -2(0,9 + x)
b. 2,3x – 2(0,7 + 2x) = 3,6 – 1,7x
c. 3(2,2 – 0,3x) = 2,6 + (0,1x – 4)
d. 3,6 – 0,5(2x + 1) = x – 0,25(2 – 4x)
Lời giải:
a. 1,2 – (x – 0,8) = -2(0,9 + x) ⇔ 1,2 – x + 0,8 = -1,8 – 2x
⇔ -x + 2x = -1,8 – 2 ⇔ x = -3,8
Phương trình có nghiệm x = -3,8
b. 2,3x – 2(0,7 + 2x) = 3,6 – 1,7x
⇔ 2,3x – 1,4 – 4x = 3,6 – 1,7x ⇔ 2,3x – 4x + 1,7x = 3,6 + 1,4
⇔ 0x = 5
Phương trình vô nghiệm
c. 3(2,2 – 0,3x) = 2,6 + (0,1x – 4)
⇔ 6,6 – 0,9x = 2,6 + 0,1x – 4 ⇔ 6,6 – 2,6 + 4 = 0,1x + 0,9x
⇔ x = 8
Phương trình có nghiệm x = 8
d. 3,6 – 0,5(2x + 1) = x – 0,25(2 – 4x)
⇔ 3,6 – x – 0,5 = x – 0,5 + x ⇔ 3,6 – 0,5 + 0,5 = x + x + x
⇔ 3,6 = 3x ⇔ 1,2
Phương trình có nghiệm x = 1,2
Bài 20 trang 8 sách bài tập Toán 8 Tập 2: Giải các phương trình sau
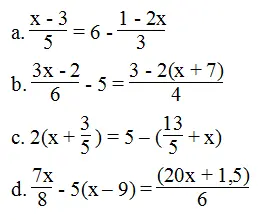
Lời giải:
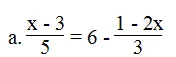
⇔ 3(x – 3) = 6.15 – 5(1 – 2x)
⇔ 3x – 9 = 90 – 5 + 10x
⇔ 3x – 10x = 90 – 5 + 9
⇔ -7x = 94 ⇔ x = – 94/7
Phương trình có nghiệm x = – 94/7
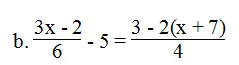
⇔ 2(3x – 2) – 5.12 = 3[3 – 2(x + 7)]
⇔ 6x – 4 – 60 = 9 – 6(x + 7)
⇔ 6x – 64 = 9 – 6x – 42
⇔ 6x + 6x = 9 – 42 + 64
⇔ 12x = 31 ⇔ x = 31/12
Phương trình có nghiệm x = 31/12
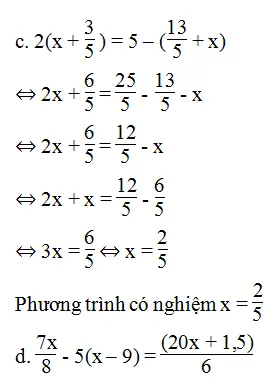
⇔ 3.7x – 24.5(x – 9) = 4(20x + 1,5)
⇔ 21x – 120(x – 9) = 80x + 6
⇔ 21x – 120x + 1080 = 80x + 6
⇔ 21x – 120x – 80x = 6 – 1080
⇔ -179x = -1074 ⇔ x = 6
Phương trình có nghiệm x = 6.
Bài 21 trang 8 sách bài tập Toán 8 Tập 2: Tìm điều kiện của x để giá trị mỗi phân thức sau xác định:
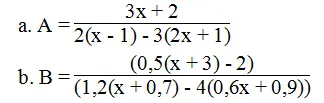
Lời giải:
a. Phân thức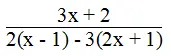 
xác định khi:
2(x – 1) – 3(2x + 1) ≠ 0
Ta giải phương trình: 2(x – 1) – 3(2x + 1) = 0
Ta có: 2(x – 1) – 3(2x + 1) = 0 ⇔ 2x – 2 – 6x – 3 = 0
⇔ -4x – 5 = 0 ⇔ 4x = -5 ⇔ x = -54
Vậy khi x ≠ -54 thì phân thức A xác định.
b. Phân thức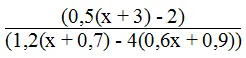 
xác định khi:
1,2(x + 0,7) – 4(0,6x + 0,9) ≠ 0
Ta giải phương trình: 1,2(x + 0,7) – 4(0,6x + 0,9) = 0
Ta có: 1,2(x + 0,7) – 4(0,6x + 0,9) = 0
⇔ 1,2x + 0,84 – 2,4 – 3,6 = 0
⇔ -1,2x – 2,76 = 0 ⇔ x = -2,3
Vậy khi x ≠ -2,3 thì phân thức B xác định.
Bài 22 trang 8 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:
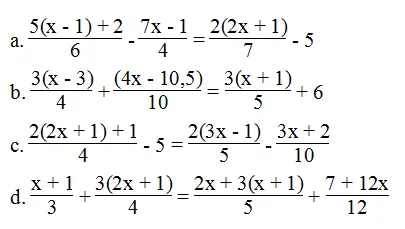
Lời giải:
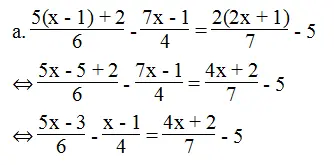
⇔ 14(5x – 3) – 21(7x – 1) = 12(4x + 2) – 5.84
⇔ 70x – 42 – 147x + 21 = 48x + 24 – 420
⇔ 70x – 147x – 48x = 24 – 420 + 42 – 21
⇔ -125x = -375 ⇔ x = 3
Phương trình có nghiệm x = 3
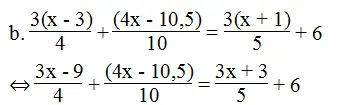
⇔ 5(3x – 9) + 2(4x – 10,5) = 4(3x + 3) + 6.20
⇔ 15x – 45 + 8x – 21 = 12x + 12 + 120
⇔ 15x + 8x – 12x = 12 + 120 + 45 + 21 ⇔ 11x = 198 ⇔ x = 18
Phương trình có nghiệm x = 18
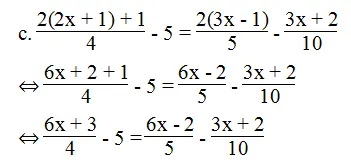
⇔ 5(6x + 3) – 5.20 = 4(6x – 2) – 2(3x + 2)
⇔ 30x + 15 – 100 = 24x – 8 – 6x – 4
⇔ 30x – 24x + 6x = -8 -4 – 15 + 100
⇔ 12x = 73 ⇔ x = 73/12
Phương trình có nghiệm x = 73/12
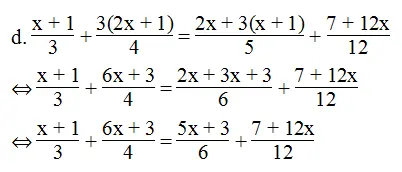
⇔ 4(x + 1) + 3(6x + 3) = 2(5x + 3) + 7 + 12x
⇔ 4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x
⇔ 4x + 18x – 10x – 12x = 6 + 7 – 4 – 9 ⇔ 0x = 0
Phương trình có vô số nghiệm.
Bài 23 trang 8 sách bài tập Toán 8 Tập 2: Tìm giá trị của k sao cho:
a. Phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40 có nghiệm x = 2.
b. Phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k) có nghiệm x = 1.
Lời giải:
a. Thay x = 2 vào phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40, ta có:
(2.2 + 1)(9.2 + 2k) – 5(2 + 2) = 40
⇔ (4 + 1)(18 + 2k) – 5.4 = 40 ⇔ 5(18 + 2k) – 20 = 40
⇔ 90 + 10k – 20 = 40 ⇔ 10k = 40 – 90 + 20 ⇔ 10k = -30
⇔ k = -3
Vậy khi k = -3 thì phương trình (2x + 1)(9x + 2k) – 5(x + 2) = 40 có nghiệm x = 2.
b. Thay x = 1 vào phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k), ta có:
2(2.1 + 1) + 18 = 3(1 + 2)(2.1 + k)
⇔ 2(2 + 1) + 18 = 3.3(2 + k) ⇔ 2.3 + 18 = 9(2 + k)
⇔ 6 + 18 = 18 + 9k ⇔ 24 – 18 = 9k ⇔ 6 = 9k ⇔ k = 69 = 23
Vậy khi k = 23 thì phương trình 2(2x + 1) + 18 = 3(x + 2)(2x + k) có nghiệm x = 1.
Bài 24 trang 8 sách bài tập Toán 8 Tập 2: Tìm các giá trị của x sao cho hai biểu thức A và B cho sau đây có giá trị bằng nhau:
a. A = (x – 3)(x + 4) – 2(3x – 2); B = (x – 4)2
b. A = (x + 2)(x – 2) + 3x2; B = (2x + 1)2 + 2x
c. A = (x – 1)(x2 + x + 1) – 2x; B = x(x – 1)(x + 1)
d. A = (x + 1)3 – (x – 2)3; B = (3x – 1)(3x + 1)
Lời giải:
a. Ta có: A = B ⇔ (x – 3)(x + 4) – 2(3x – 2) = (x – 4)2
⇔ x2 + 4x – 3x – 12 – 6x + 4 = x2 – 8x + 16
⇔ x2 – x2 + 4x – 3x – 6x + 8x = 16 + 12 – 4
⇔ 3x = 24 ⇔ x = 8
Vậy với x = 8 thì A = B
b. Ta có: A = B ⇔ (x + 2)(x – 2) + 3x2 = (2x + 1)2 + 2x
⇔ x2 – 4 + 3x2 = 4x2 + 4x + 1 + 2x
⇔ x2 + 3x2 – 4x2 – 4x – 2x = 1 + 4 ⇔ -6x = 5 ⇔ x = – 5/6
Vậy với x = – 5/6 thì A = B.
c. Ta có: A = B ⇔ (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1) ⇔ x3 – 1 – 2x = x3 – x
⇔ x3 – x3 – 2x + x = 1 ⇔ -x = 1 ⇔ x = -1
Vậy với x = -1 thì A = B
d. Ta có: A = B ⇔ (x + 1)3 – (x – 2)3 = (3x – 1)(3x + 1)
⇔ x3 + 3x2 + 3x + 1 – x3 + 6x2 – 12x + 8 = 9x2 – 1
⇔ x3 – x3 + 3x2 + 6x2 – 9x2 + 3x – 12x = -1 – 1 – 8
⇔ -9x = -10 ⇔ x = 10/9
Vậy với x = 10/9 thì A = B.
Bài 25 trang 9 sách bài tập Toán 8 Tập 2: Giải các phương trình sau:
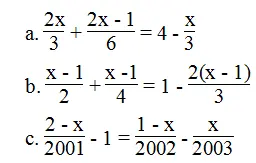
Lời giải:
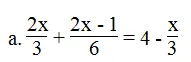
⇔ 2.2x + 2x – 1 = 4.6 – 2x
⇔ 4x + 2x – 1 = 24 – 2x
⇔ 6x + 2x = 24 + 1
⇔ 8x = 25 ⇔ x = 25/8
Phương trình có nghiệm x = 25/8
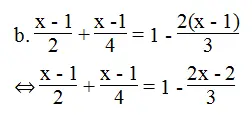
⇔ 6(x – 1) + 3(x – 1) = 12 – 4(2x – 2)
⇔ 6x – 6 + 3x – 3 = 12 – 8x + 8 ⇔ 6x + 3x + 8x = 12 + 8 + 6 + 3
⇔ 17x = 29 ⇔ x = 29/17
Phương trình có nghiệm x = 29/17
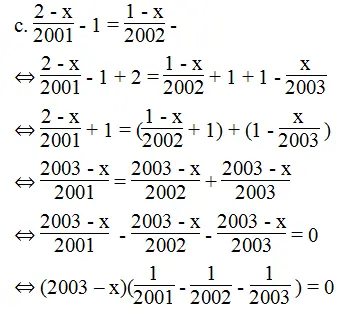
⇔ 2003 – x = 0 ⇔ x = 2003
Phương trình có nghiệm x = 2003
Bài 3.1 trang 9 sách bài tập Toán 8 Tập 2: Cho hai phương trình:
7x/8 – 5(x – 9) = 1/6(20x + 1,5) (1)
2(a – 1)x – a(x – 1) = 2a + 3 (2)
a. Chứng tỏ rằng phương trình (1) có nghiệm duy nhất, tìm nghiệm đó
b. Giải phương trình (2) khi a = 2
c. Tìm giá trị của a để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1).
Lời giải:
a. Nhân hai vế của phương trình (1) với 24, ta được:
7x/8 – 5(x – 9) = 1/6(20x + 1,5)
⇔21x − 120(x − 9) = 4(20x + 1,5)
⇔21x − 120x − 80x = 6 − 1080
⇔−179x = −1074 ⇔ x = 6
Vậy phương trình (1) có một nghiệm duy nhất x = 6.
b. Ta có:
2(a − 1) − a(x − 1) = 2a + 3
⇔(a − 2)x = a + 3 (3)
Do đó, khi a = 2, phương trình (2) tương đương với phương trình 0x = 5.
Phương trình này vô nghiệm nên phương trình (2) vô nghiệm.
c. Theo điều kiện của bài toán, nghiệm của phương trình (2) bằng một phần ba nghiệm của phương trình (1) nên nghiệm đó bằng 2.
Do (3) nên phương trình (2) có nghiệm x = 2 cũng có nghĩa là phương trình (a −2 )2 = a + 3 có nghiệm x = 2.
Thay giá trị x = 2 vào phương trình này, ta được (a − 2)2 = a + 3.
Ta coi đây là phương trình mới đối với ẩn a. Giải phương trình mới này: (a − 2)2 = a + 3 ⇔ a = 7
Khi a = 7, dễ thử thấy rằng phương trình (a − 2)x = a + 3 có nghiệm x = 2, nên phương trình (2) cũng có nghiệm x = 2.
Bài 3.2 trang 9 sách bài tập Toán 8 Tập 2: Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau:
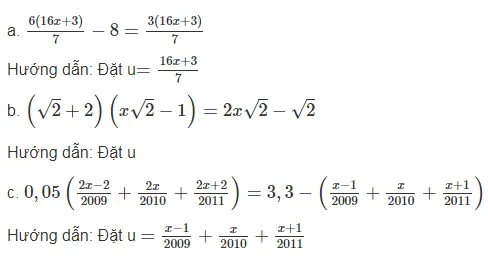
Lời giải:
a. Đặt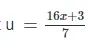 
ta có phương trình 6u – 8 = 3u + 7.
Giải phương trình này:
6u – 8 = 3u + 7
⇔ 6u – 3u = 7 + 8
⇔ 3u = 15 ⇔ u = 5
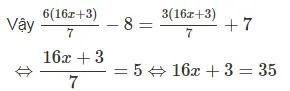
⇔16x = 32 ⇔ x = 2
b. Nếu đặt u =x√2 − 1 thì x√2 = u + 1 nên phương trình có dạng
(√2 + 2)u = 2(u + 1)−√2 (1)
Ta giải phương trình (1):
(1) ⇔√2u + 2u = 2u + 2 − √2
⇔√2u = 2−√2
⇔√2u=√2(√2 − 1)⇔u = √2 − 1
⇔(√2 + 2)(x√2 – 1) = 2x√2 – √2
⇔x√2 − 1 = √2 − 1
⇔x√2 = √2
⇔x = 1
c. Nếu đặt
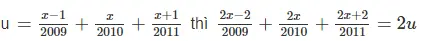nên phương trình đã cho có dạng
0,05.2u = 3,3 − u, hay 0,1u = 3,3 − u
Dễ thấy phương trình này có một nghiệm duy nhất u = 3. Do đó
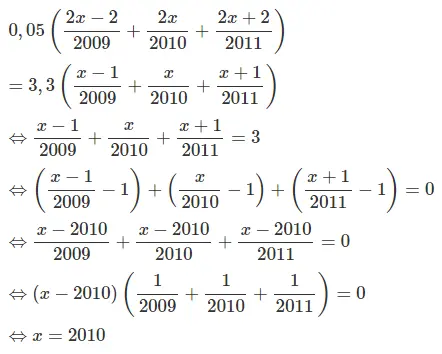
@Nguyễn Việt Anh: CTV là công tác viên