Các câu hỏi tương tự
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Cho mặt phẳng (P): x + y + 2z - 2 0 và đường thẳng (d):
x
+
2017
1
y
2
z
-
2017
1
. Góc tạo bởi (d) và (P) là
α
. Giá trị cot
α
là
Đọc tiếp
Cho mặt phẳng (P): x + y + 2z - 2 =0 và đường
thẳng (d): x + 2017 1 = y 2 = z - 2017 1 . Góc tạo bởi
(d) và (P) là α . Giá trị cot α là
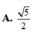
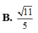
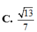
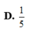
Trong không gian Oxyz, cho ba điểm M(1;2;4); N(0;1;2); P(2;1;3) và mặt phẳng
α
: x+Ay+Bx+C0 . Biết
α
song song với OP và đi qua hai điểm M, N. Giá trị của biểu thức A+B-C là A. 1. B. -1. C. -5. D. 0.
Đọc tiếp
Trong không gian Oxyz, cho ba điểm M(1;2;4); N(0;1;2); P(2;1;3) và mặt phẳng α : x+Ay+Bx+C=0 . Biết α song song với OP và đi qua hai điểm M, N. Giá trị của biểu thức A+B-C là
A. 1.
B. -1.
C. -5.
D. 0.
Cho hàm số y x3-3x2 .Tìm tất cả các giá trị thực tham số m để đường thẳng đi qua 2 điểm cực trị của đồ thị C tạo với đường thẳng x+ my+ 30 một góc α biết cosα 4/5. A. m 2 hoặc m -2/11. B. m -2 hoặc m -2/11. C. m 2 hoặc m 2/11. D. m2
Đọc tiếp
Cho hàm số y= x3-3x2 .Tìm tất cả các giá trị thực tham số m để đường thẳng đi qua 2 điểm cực trị của đồ thị C tạo với đường thẳng x+ my+ 3=0 một góc α biết cosα= 4/5.
A. m= 2 hoặc m = -2/11.
B. m= -2 hoặc m = -2/11.
C. m= 2 hoặc m = 2/11.
D. m=2
Cho hàm số y x3-3x2-mx+2 với m là tham số thực. Tìm giá trị của m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng d ; x+4y-50 một góc
α
45
°
. A. m -1/2 B. m 1/2 C. m0 D. m 1
Đọc tiếp
Cho hàm số y= x3-3x2-mx+2 với m là tham số thực. Tìm giá trị của m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng d ; x+4y-5=0 một góc α = 45 ° .
A. m= -1/2
B. m= 1/2
C. m=0
D. m= 1
Viết phương trình tham số của đường thẳng d trong mỗi trường hợp sau: d đi qua A(2; -1; 3) và vuông góc với mặt phẳng (α): x + y – z + 5 = 0.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
α
: x+y+z-30 và đường thẳng
d
:
x
1
y
+
1
2
z
-
2
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x+y+z-3=0 và đường thẳng d : x 1 = y + 1 2 = z - 2 - 1 . Gọi ∆ là hình chiếu vuông góc của d trên α và u → = ( 1 ; a ; b ) là một vectơ chỉ phương của ∆ với a, b ∈ ℤ . Tính tổng a+b.
A. 0
B. 1
C. -1
D. -2
Xét vị trí tương đối của đường thẳng d với mặt phẳng (
α
) trong các trường hợp sau:
d
:
x
2
-
t
y
t
z...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng ( α ) trong các trường hợp sau:
d : x = 2 - t y = t z = 2 + t và ( α ): x + z + 5 = 0
1.Giải phương trình sau: (x+1) (x+2) = (2-x) (x+2)
2.Tìm các giá trị của m sao cho mỗi biểu thức sau có giá trị bằng 5
a, 2(m+3/5) - (m+13/5)
b, 2(3m+1)+1/4 - 2(3m-1)/5+3m+2/10

