Các câu hỏi tương tự
Biết phương trình
z
2
+
a
z
+
b
0
(
b
,
c
∈
R
)
có một nghiệm z1-i. Tính môđun của số phức wa+bi.
Đọc tiếp
Biết phương trình z 2 + a z + b = 0 ( b , c ∈ R ) có một nghiệm z=1-i. Tính môđun của số phức w=a+bi.
![]()
![]()
![]()
![]()
Tìm hai số thực b và c biết rằng phương trình
z
2
+
b
z
+
c
0
có nghiệm phức z 1+i
Đọc tiếp
Tìm hai số thực b và c biết rằng phương trình z 2 + b z + c = 0 có nghiệm phức z = 1+i
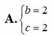
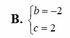
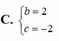
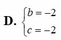
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
nhận
z
2
và
z
1
+
i
làm các nghiệm của phương trình. Khi đó
a
-
b
+
c
là
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
![]()
![]()
![]()
![]()
Cho
a
,
b
,
c
∈
R
;
a
≠
0
;
b
2
-
4
a
c
0
. Tìm số nghiệm phức của phương trình
a
z
2
+
b
z
+
c
0
(với ẩn là z) A. 3 B...
Đọc tiếp
Cho a , b , c ∈ R ; a ≠ 0 ; b 2 - 4 a c < 0 . Tìm số nghiệm phức của phương trình a z 2 + b z + c = 0 (với ẩn là z)
A. 3
B. 2
C. 1
D. 0
Phương trình
z
2
+
b
z
+
c
0
có một nghiệm phức là
z
1
-
2
i
.Tích của hai số b và c bằng A. 3 B.-10 C.-2 và 5 D. 5
Đọc tiếp
Phương trình z 2 + b z + c = 0 có một nghiệm phức là z = 1 - 2 i .Tích của hai số b và c bằng
A. 3
B.-10
C.-2 và 5
D. 5
Biết rằng phương trình z 2 + bz + c = 0(b,c ∈ ℝ ) có một nghiệm phức là z 1 = 1 + 2i. Khi đó
A. b + c = 0
B. b + c = 3
C. b + c = 2
D. b + c = 7
Giá trị của các số thực b, c để phương trình
z
2
+
b
z
+
c
0
nhận số phức
z
1
+
i
làm một nghiệm là: A.
b
2
c...
Đọc tiếp
Giá trị của các số thực b, c để phương trình z 2 + b z + c = 0 nhận số phức z = 1 + i làm một nghiệm là:
A. b = 2 c = - 2
B. b = - 2 c = - 2
C. b = - 2 c = 2
D. b = 2 c = 2
Giá trị của các số thực b ; c để phương trình z2 + bz + c 0 nhận số phức z 1 + i làm một nghiệm là: A. B. C. D.
Đọc tiếp
Giá trị của các số thực b ; c để phương trình z2 + bz + c = 0 nhận số phức z =1 + i làm một nghiệm là:
A. 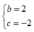
B. 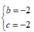
C. 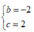
D. 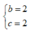
Tìm các số thực a,b,c để phương trình (ẩn z)
z
3
+
a
z
2
+
b
z
+
c
0
nhận
z
1
+
i
và
z
2
làm nghiệm
Đọc tiếp
Tìm các số thực a,b,c để phương trình (ẩn z) z 3 + a z 2 + b z + c = 0 nhận z = 1 + i và z = 2 làm nghiệm
![]()
![]()
![]()
![]()


