Chọn A.
Điều kiện: ![]()
Phương trình
![]()
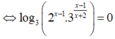
![]()
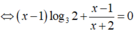
![]()
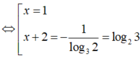
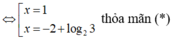
Do đó S = -1 + log23 = log23 – log22 = log23/2.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Chọn A.
Điều kiện: ![]()
Phương trình
![]()
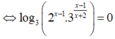
![]()
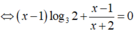
![]()
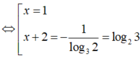
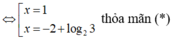
Do đó S = -1 + log23 = log23 – log22 = log23/2.
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x 0 . Giá trị của a + b - x 0 bằng:
A. 100
B. 30
C. 150
D. 50
Biết rằng phương trình 2 x 2 - 4 x + 2 = 2 x - 4 có hai nghiệm phân biệt là x1; x2 . Tính giá trị của biểu thức S = x 1 4 + x 4 2
A. 17
B. 97
C . 82
D. 257
cho hai số a,b là hai số thực đều lớn hơn 1. giá trị nhỏ nhất của biểu thức s=
\(\dfrac{1}{log_{b\sqrt[3]{a}}}\)+\(\dfrac{1}{log\sqrt[3]{ab^2}}\)
Biết rằng phương trình 3 + 5 2 + 3 3 - 5 2 = 2 x + 2 có hai nghiệm phân biệt là x 1 > x 2 . Nghiệm x 1 có dạng log a + b 5 2 9 , với a; b nguyên dương. Tính S = a4 + 10ab
A. 2611
B. 2681
C. 2422
D. 2429
Gọi x 1 , x 2 là hai nghiệm của phương trình log 2 x + log 3 x . log 27 - 4 = 0 .Giá trị của biểu thức log x 1 + log x 2 bằng
A. 3
B. -3
C. -4
D. 4
Cho f x = a ln x + x 2 + 1 + b sin x + 6 với a , b ∈ ℝ . Biết rằng f(log(log e)) = 2. Tính giá trị của f(log(ln10)).
A. 10
B. 2
C. 4
D. 8
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa mãn x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d.
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Gọi x 1 , x 2 ( x 1 < x 2 ) là 2 nghiệm của phương trình ( 3 - 8 ) x 3 + ( ( 3 - 8 ) 3 ) x = 6 . Biểu thức P = 2 x 1 + x 2 2 có giá trị là
A. -3
B. 0
C. 3
D. 15
Câu 11: Nghiệm của phương trình \(\log^2_{\frac{1}{2}} (x-2)-(2-x)\log_{2} (x-2)+3(x-5)=0\) là?