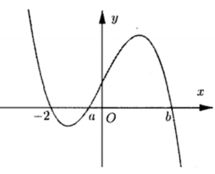
Đáp án A
Phương pháp:
Đặt Đáp án A
Phương pháp:
Đặt f(x) = a(x – x1)(x – x2)(x – x3)(x – x4), tính đạo hàm của hàm số y = f(x)
Xét hàm số h x = f ' x f x và chứng minh f(x).f’’(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Cách giải: Đồ thị hàm sốy = f(x) cắt trục hoành tại bốn điểm phân biệt nên
f(x) = a(x – x1)(x – x2)(x – x3)(x – x4)
=> f ’(x) = a(x – x1)(x – x2)(x – x3)(x – x4) + a(x – x1)(x – x3)(x – x4) + a(x – x1)(x – x2)(x – x4) + a(x – x1)(x – x2)(x – x3)
f ’(x) = f(x) 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4 => f’(x) ≠ 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Đặt h x = f ' x f x = 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Ta có
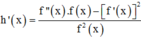
= - 1 ( x - x 1 ) 2 + - 1 ( x - x 2 ) 2 + - 1 ( x - x 3 ) 2 + - 1 ( x - x 4 ) 2 <0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> f ''(x).f(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> g(x) = [f’(x)]2 – f(x).f’’(x)>0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Khi f(x) = 0 => f '(x) ≠ 0 => g(x) = [f’(x)]2 – f(x).f’’(x) ≠ 0
Vậy đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) không cắt trục Ox