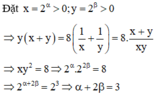Các câu hỏi tương tự
Biết rằng
α
;
β
là các số thực thỏa mãn
2
β
2
α
+
2
β
8
2
-
α
+
2
-...
Đọc tiếp
Biết rằng α ; β là các số thực thỏa mãn 2 β 2 α + 2 β = 8 2 - α + 2 - β . Giá trị của α + 2 β bằng
A. 1
B. 2
C. 4
D. 3
Cho
α
,
β
thỏa mãn
sin
α
+
sin
β
2
2
;
cos
α
+
cos
β
6
2
. Tính
cos
α...
Đọc tiếp
Cho α , β thỏa mãn sin α + sin β = 2 2 ; cos α + cos β = 6 2 . Tính cos α - β .
A. cos α - β = 0
B. cos α - β = 2 2
C. cos α - β = 3 2
D. cos α - β = 1 2
Cho hàm số f(x) liên tục trên đoạn [0;1] thoả mãn với mọi
x
,
y
,
α
,
β
∈
[
0
;
1
]
và
α
2
+
β
2
0
ta có
α
f
(
x
)
+
β
f
(
y
)
≥
(
α
+
β...
Đọc tiếp
Cho hàm số f(x) liên tục trên đoạn [0;1] thoả mãn với mọi x , y , α , β ∈ [ 0 ; 1 ] và α 2 + β 2 > 0 ta có α f ( x ) + β f ( y ) ≥ ( α + β ) f α x + β y α + β . Biết f(0)=0, ∫ 0 1 2 f ( x ) d x = 2 . Giá trị nhỏ nhất của tích phân ∫ 0 1 f ( x ) d x bằng
A. 8.
B. 4.
C. 2 2 .
D. 2.
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(10;6;-2),B(5;10;-9) và mặt phẳng (P):2x+2y+z-120. Gọi M(a;b;c) là điểm di động trên mặt phẳng (P) sao cho MA, MB tạo với m.t ph.ng (P) các góc
α
,
β
thỏa mãn
α
+
β
90
°
. Khi biểu thức T4MA+MB đạt giá trị nhỏ nhất. Giá trị của biểu thức a+b+c bằng A. 15. B. 3. C. 5. D. 13.
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(10;6;-2),B(5;10;-9) và mặt phẳng (P):2x+2y+z-12=0. Gọi M(a;b;c) là điểm di động trên mặt phẳng (P) sao cho MA, MB tạo với m.t ph.ng (P) các góc α , β thỏa mãn α + β = 90 ° . Khi biểu thức T=4MA+MB đạt giá trị nhỏ nhất. Giá trị của biểu thức a+b+c bằng
A. 15.
B. 3.
C. 5.
D. 13.
Trong không gian Oxyz, cho hai mặt phẳng (
α
): x+y+z-10 và (
β
): 2x-y+mz-m+10, với m là tham số thực. Giá trị của m để (
α
)
⊥
(
β
) là A. -1 B. 0 C. 1 D.-4
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng ( α ): x+y+z-1=0 và ( β ): 2x-y+mz-m+1=0, với m là tham số thực. Giá trị của m để ( α ) ⊥ ( β ) là
A. -1
B. 0
C. 1
D.-4
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có ABBC, BC3cm. Hai mặt phẳng (ACC’A’) và (BDD’B’) hợp với nhau góc
α
0
≤
α
≤
π
2
Đường chéo B’D hợp với mặt phẳng (CDD’C’) một góc
β
0
≤
β
≤
π
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB<BC, BC=3cm. Hai mặt phẳng (ACC’A’) và (BDD’B’) hợp với nhau góc α 0 ≤ α ≤ π 2 Đường chéo B’D hợp với mặt phẳng (CDD’C’) một góc β 0 ≤ β ≤ π 2 . Hai góc α , β thay đổi nhưng thỏa mãn hình hộp ADD’A’.BCC’B’ luôn là hình lăng trụ đều. Giá trị lớn nhất thể tích của khối hộp ABCD.A’B’C’D’ là
![]()
![]()
![]()
![]()
Cho 0a,b,c,x
≢
1
. Biết
log
a
x
α
,
log
b
x
β
,
log
c
x
γ
, tính
log
a
b
c
x
theo
α
,
β
,
γ
. A.
log
a
b
c
x...
Đọc tiếp
Cho 0<a,b,c,x ≢ 1 . Biết log a x = α , log b x = β , log c x = γ , tính log a b c x theo α , β , γ .
A. log a b c x = α + β + γ
B. log a b c x = α β γ
C. log a b c x = α β + β γ + γ α α β γ
D. log a b c x = α β γ α β + β γ + γ α
Phương trình
2
sin
2
2
x
−
5
sin
2
x
+
2
0
có hai họ nghiệm dạng
x
α
+
kπ
,
x
β
+
kπ
0
α
,
β
π
. Khi đó...
Đọc tiếp
Phương trình 2 sin 2 2 x − 5 sin 2 x + 2 = 0 có hai họ nghiệm dạng x = α + kπ , x = β + kπ 0 < α , β < π . Khi đó tích αβ là
A. 5 π 2 36
B. 5 π 2 144
C. - 5 π 2 36
D. - 5 π 2 144