Chọn đáp án A.
Vì M x 1 ; y 1 , N x 2 ; y 2 là các điểm cực trị của đồ thị hàm số nên y ' x 1 = y ' x 2 = 0
do đó x 1 , x 2 là hai nghiệm phân biệt của y ' = 3 x 2 + 2 a x + b = 0
Ta có phân tích: x 3 + a x 2 + b x + c
Do đó y 1 = 2 3 b - a 2 3 x 1 + c - a b 9
y 2 = 2 3 b - a 2 3 x 2 + c - a b 9
Vì 3 x 1 2 + 2 a x 1 + b = 0 ; 3 x 2 2 + 2 a x 2 + b = 0
Vậy điều kiện bài toán tương đương với
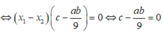
⇔ a b = 9 c
Khi đó:
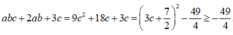
Dấu bằng đạt tại c = - 7 6 ; a b = - 21 2