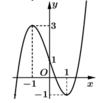
Đáp án B
Ta có ∫ 1 e x + 1 ln x + 2 1 + x ln x d x = ∫ 1 e 1 + x ln x + 1 + ln x 1 + x ln x d x = ∫ 1 e 1 + 1 + ln x 1 + x ln x d x = ∫ 1 e d x + ∫ 1 e 1 + ln x 1 + x ln x d x
= x 1 e + ∫ 1 e d 1 + x ln x 1 + x ln x = e − 1 + ln 1 + x ln x 1 e = e − 1 + ln e + 1 = e + ln e + 1 e ⇒ a = 1 b = 1 .
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Cho hai số thực không âm x,y ≤ 1. Biết P = l n ( 1 + x 2 ) ( 1 + y 2 ) + 8 17 ( x + y ) 2 có giá trị nhỏ nhất là - a b + 2 ln c d trong đó a, b, c, d là số tự nhiên thỏa mãn ước chung của (a,b) = (c,d) = 1. Giá trị của a+b+c+d là
A. 406
B. 56
C. 39
D. 405
Cho tích phân I = ∫ 0 1 ( x + 2 ) ln ( x + 1 ) d x = a l n 2 − 7 b trong đó a, b là các số nguyên dương. Tổng a + b 2 bằng
A. 8
B. 16
C. 12
D. 20
Tìm nguyên hàm của hàm số f ( x ) = 2008 + ln 2 x x có
dạng F ( x ) = a ln x + ln x 3 b + C . Khi đó tổng S
= a + b là?
A. 2012
B. 2010
C. 2009
D. 2011
Cho 2 đường thẳng d 1 : x 2 = y - 1 1 = z + 1 - 1 , d 2 : x = 1 + t y = - 1 - 2 t z = 2 + t . Gọi M a ; b ; c là điểm thuộc d 1 và N d , e , f là điểm thuộc d 2 sao cho MN ngắn nhất, khi đó tổng a + b + c + d + e + f bằng
A. 11 7
B. - 10 7
C. - 11 7
D. 10 7
Biết ∫ 1 3 2 + ln ( x + 3 ) ( x + 1 ) 2 dx =a ln2+b ln3+c (a,b,c∈Q). Giá trị 3a-b+2c bằng
A. 7.
B. 0.
C. -2.
D. -11/2
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
Đường thẳng x = k cắt đồ thị hàm số y = log 5 x và đồ thị hàm số y = log 3 ( x + 4 ) . Khoảng cách giữa các giao điểm là 1/2. Biết k = a + b , trong đó a, b là các số nguyên. Khi đó tổng a + b bằng
A. 7
B. 6
C. 8
D. 5
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
