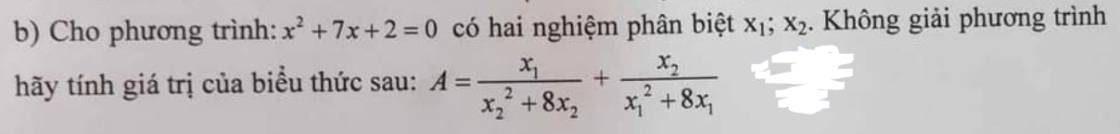Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-7\\x_1x_2=2\end{matrix}\right.\)
Khi đó: \(A=\dfrac{x_1}{x_2^2+8x_2}+\dfrac{x_2}{x_1^2+8x_1}\)
\(=\dfrac{x_1\left(x_1^2+8x_1\right)}{\left(x_2^2+8x_2\right)\left(x_1^2+8x_1\right)}+\dfrac{x_2\left(x_2^2+8x_2\right)}{\left(x_1^2+8x_1\right)\left(x^2_2+8x_2\right)}\)
\(=\dfrac{x_1^3+8x_1^2+x_2^3+8x^2_2}{\left(x_1^2+8x_1\right)\left(x_2^2+8x_2\right)}\)
\(=\dfrac{\left(x_1^3+x_2^3\right)+8\left(x_1^2+x_2^2\right)}{x_1^2x_2^2+8x_1^2x_2+8x_1x_2^2+64x_1x_2}\)
\(=\dfrac{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)+8\left(x_1+x_2\right)^2-16x_1x_2}{\left(x_1x_2\right)^2+8x_1x_2\left(x_1+x_2\right)+64x_1x_2}\)
\(=\dfrac{\left(-7\right)^3-3\cdot2\cdot\left(-7\right)+8\cdot\left(-7\right)^2-16\cdot2}{2^2+8\cdot2\cdot\left(-7\right)+64\cdot2}\)
\(=\dfrac{59}{20}\)