Câu IV: (hình bạn tự vẽ nhá)
a) Xét tam giác ABH vuông tại H và tam giác CBA vuông tại A :
Góc B chung
Góc AHB = Góc CAB = (90o)
=> Tam giác ABH ~ Tam giác CBA (g-g)
=> \(\dfrac{AH}{BH}\)= \(\dfrac{AC}{AB}\) (1)
Xét tam giác ACH vuông tại H và tam giác BCA vuông tại A:
Góc C chung
Góc AHC= Góc BAC (=90o)
=> Tam giác ACH ~ Tam giác BCA (g-g)
=> \(\dfrac{CH}{AH}\)= \(\dfrac{AC}{AB}\) (2)
Từ (1) và (2) suy ra \(\dfrac{AH}{BH}\) = \(\dfrac{CH}{AH}\) => AH2 = BH.CH
b) Áp dụng định lý Pytago trong tam giác ABC vuông tại A:
AB2 + AC2 = BC2
212 + 282 = BC2
=> BC = \(\sqrt{21^2+28^2}\)= 35(cm)
AD là tia phân giác góc BAC (GT)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CD}\) => \(\dfrac{AB}{AC+AB}\)= \(\dfrac{BD}{BD+CD}\)
=> \(\dfrac{AB}{AB+AC}\) = \(\dfrac{BD}{BC}\)
=> \(\dfrac{21}{21+28}\) = \(\dfrac{BD}{35}\)
=> BD = 35 . 21 : (21+28) = 15(cm)
=> DC = BC - BD = 35 - 15 = 20 (cm)
c) DE //AB (GT)
=> Tam giác CAB ~ Tam giác CED
=> (\(\dfrac{BC}{DC}\)) 2 = \(\dfrac{S_{CAB}}{S_{CED}}\)<=> (\(\dfrac{7}{4}\))2 = \(\dfrac{49}{16}\)= \(\dfrac{\left(AB.AC\right):2}{S_{CED}}\)
<=> \(\dfrac{49}{16}\) = \(\dfrac{\left(21.28\right):2}{S_{CED}}\)
<=> \(\dfrac{49}{16}\)= \(\dfrac{294}{S_{CED}}\)
=> SCED = \(\dfrac{16.294}{94}\)= 96 (cm2)
 Bạn nào giúp mình câu
Bạn nào giúp mình câu 
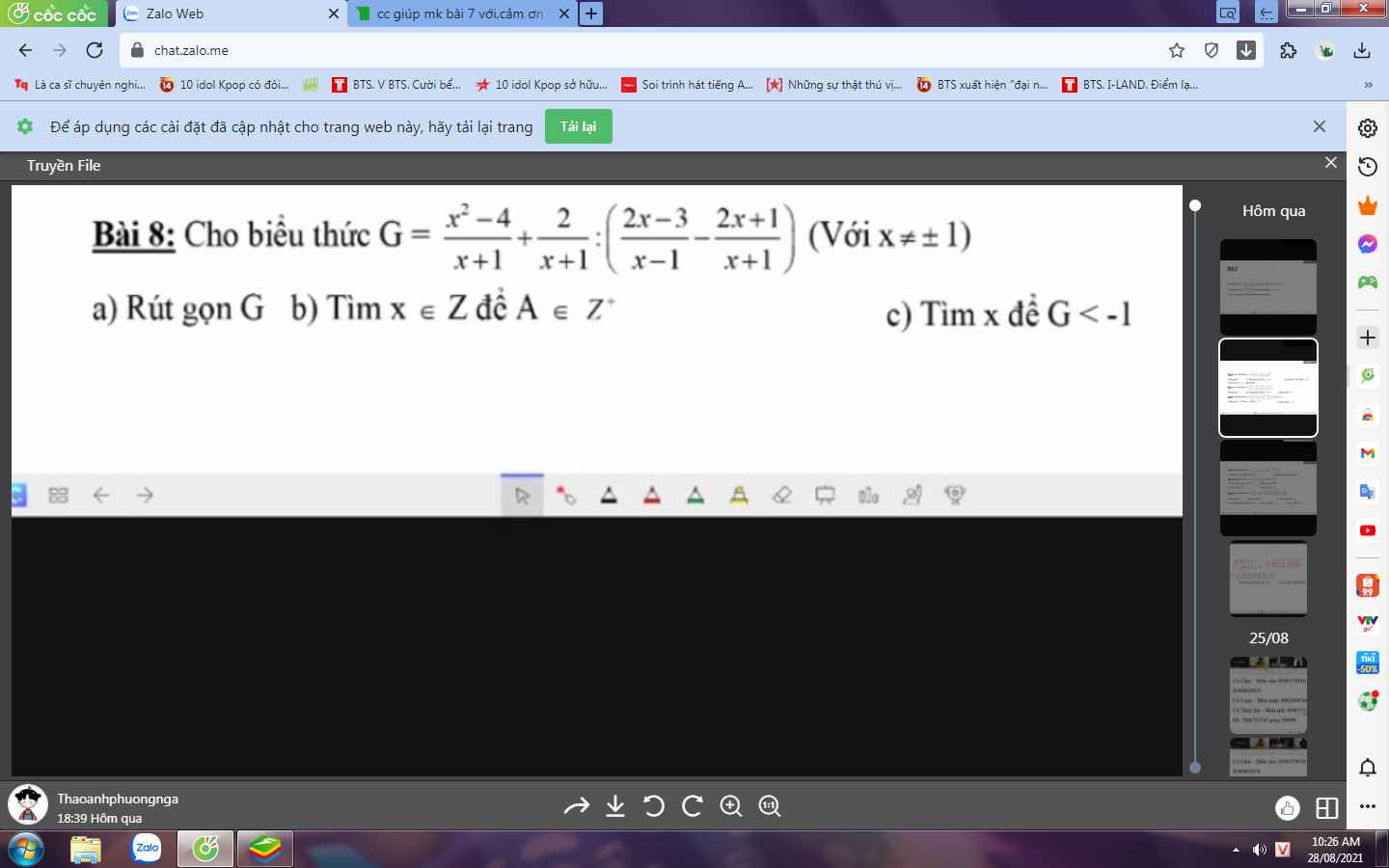
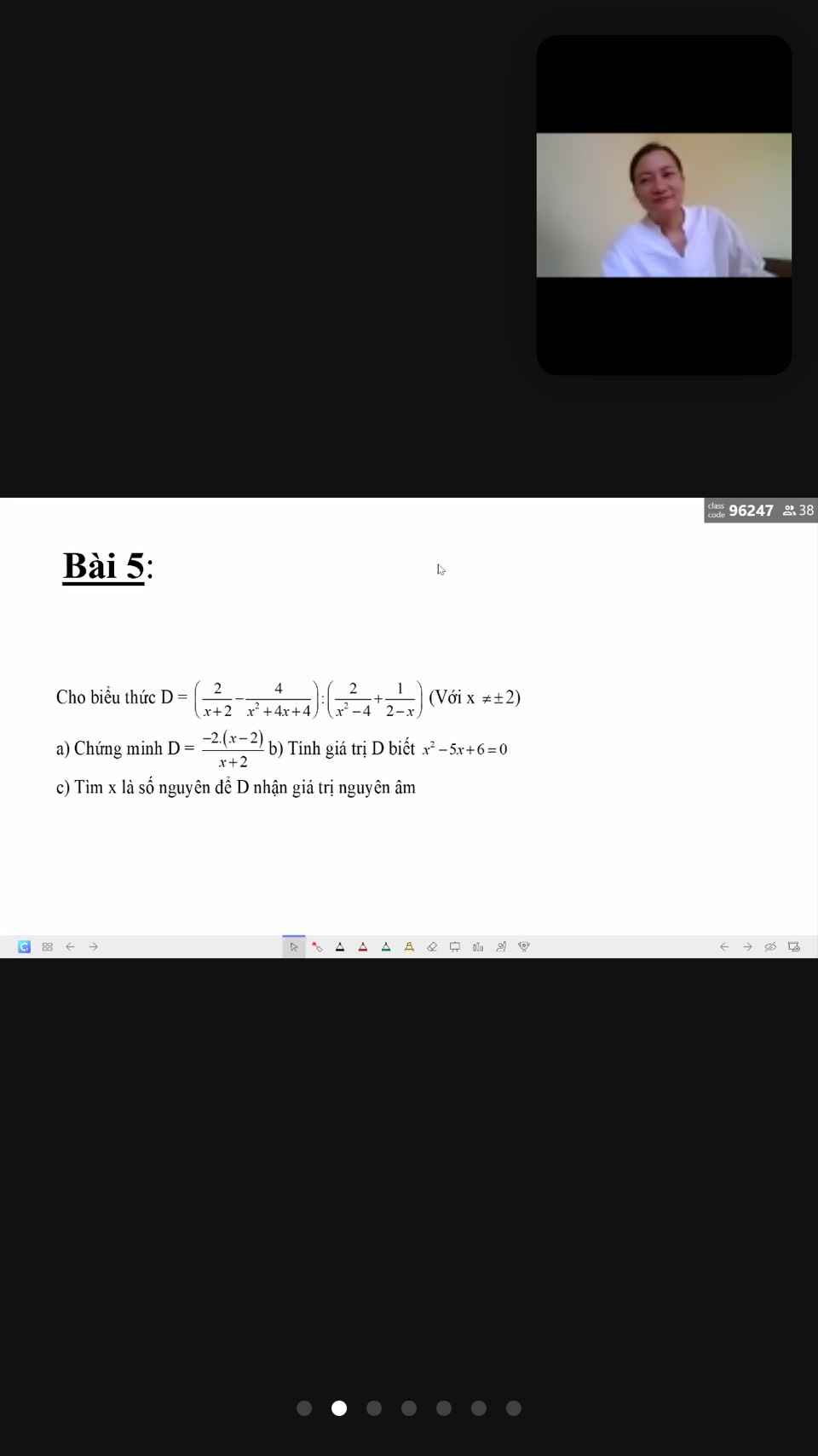 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá Giúp mình bài 4 nhe
Giúp mình bài 4 nhe