Question

Bán kính hình tròn B gấp 3 lần bán kính hình tròn A. Nếu hình A lăn xung quanh hình B, nó phải thực hiện bao nhiêu vòng quay để trở lại điểm xuất phát?

 

Answer 1

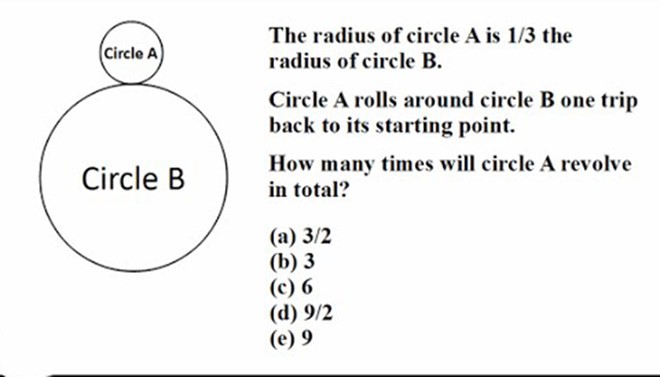
Lời giải:
Gọi tâm của hình A là $I_A$ và tâm của hình B là $I_B$. Khi đó khoảng cách của $I_A$ và $I_B$ là $r_A+r_B=r_A+3r_A=4r_A$.

Do đó $I_A$ nằm trên đường tròn bán kính $4r_A$ 

 Việc hình A lăn hết xung quanh hình B từ đầu đến điểm xuất phát giống như việc điểm $I_A$ di chuyển tròn 1 vòng trên một đường tròn bán kính $4r_A$. Độ dài quãng đường mà điểm $I_A$ phải di chuyển là: $4r_A.2\pi = 8r_A\pi$
Chu vi của hình A: $r_A.2.\pi =2r_A\pi$

Vậy hình A phải lăn số vòng để quay trở lại điểm xuất phát là:

$\frac{8r_A\pi}{2r_A\pi}=4$ (vòng)