Bài 4: Tính chất ba đường trung tuyến của tam giác
Các câu hỏi tương tự
Bài 1: Cho tam giác ABC cân tại A, vẽ AH vuông góc với BC tại H. Gọi D làtrung điểm của cạnh AC, E là giao điểm của AH và BD. Chứng minh rằng E làtrọng tâm của tam giác ABC.Bài 2: Cho tam giác ABC, AM là đường trung tuyến và G là trọng tâm. Đườngthẳng m qua M (m khác BC và AM). Vẽ BD vuông góc với m tại D, CE vuông gócvới m tại E. Chứng minh rằng G là trọng tâm của tam giác ADE.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, vẽ AH vuông góc với BC tại H. Gọi D là
trung điểm của cạnh AC, E là giao điểm của AH và BD. Chứng minh rằng E là
trọng tâm của tam giác ABC.
Bài 2: Cho tam giác ABC, AM là đường trung tuyến và G là trọng tâm. Đường
thẳng m qua M (m khác BC và AM). Vẽ BD vuông góc với m tại D, CE vuông góc
với m tại E. Chứng minh rằng G là trọng tâm của tam giác ADE.
Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến cắt nhau tại G
a) Chứng minh AM vuông góc BC
b) Cho AB = AC = 13cm, BC = 10cm, tính AG
c) Lấy I là trung điểm AB, chứng minh C, G, I thẳng hàng
Cho tam giác ABC cân tai A có AH là đường trung tuyến ứng với cạnh BC A)chứng minh tâm giác AHB=tam giác AHC B)kẻ các đường trung tuyến BM và CN .Gọi G là trọng tâm của tam giác ABC Chứng minh tam giác GBC là tam giác cân C)qua C kẻ đường thẳng vuông góc với BC cắt đường thẳng BM tại từ G kẻ đường thẳng song song với BC. Chứng minh BC=2×GD
Cho tam giác abc có 3 góc nhọn.vẽ trung tuyến am, lấy g là trọng tâm
a)so sánh độ dài của gm với ag
b)trên tia am lấy điểm d sao cho m là trung điểm của gd chứng minh ga=gd rồi chứng minh cg là trung tuyến của tam giác cad
c)tia cg cắt ab tại h. chứng minh h là trung điểm của ab
Cho tam giác ABC.Vẽ trung tuyến BM.Trên tía BM lấy G và K sao cho BG=2/3BM và G là trung điểm của BK.Gọi N là trung điểm của KC,GN cắt CM ở O .Chứng minh
a)O là trọng tâm tam giác GKC
b)GO=1/3 BC
giải hộ mình với
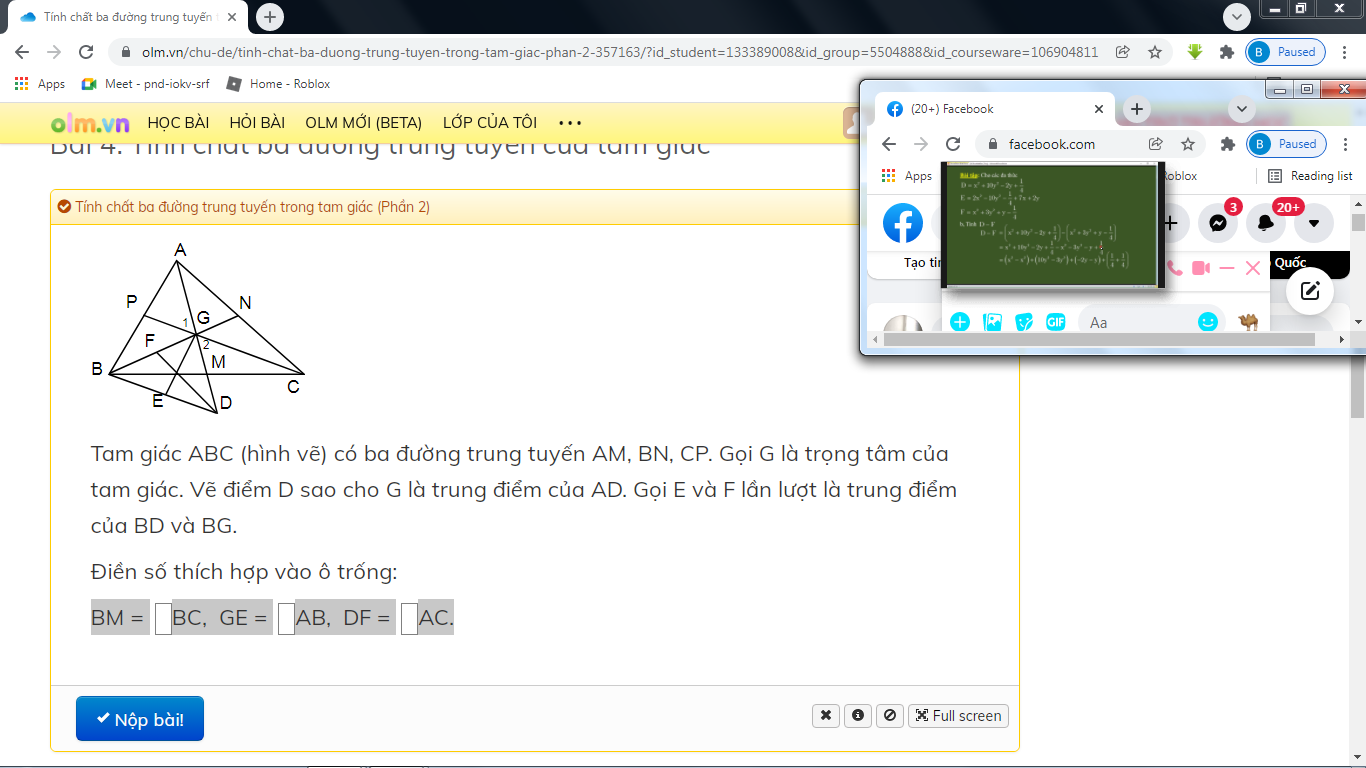
Tam giác ABC (hình vẽ) có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Gọi E và F lần lượt là trung điểm của BD và BG.
Điền số thích hợp vào ô trống:
BM =....BC, GE =.....AB, DF =........AC
Theo kết quả của bài 64 chương II, phần Hình học, SBT Toán 7 một ta có :
Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
Vận dụng kết quả trên để giải bài toán sau : Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng :
a) IK // DE, IK DE
b) AGdfrac{2}{3}AD
Đọc tiếp
Theo kết quả của bài 64 chương II, phần Hình học, SBT Toán 7 một ta có :
Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
Vận dụng kết quả trên để giải bài toán sau : Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng :
a) IK // DE, IK = DE
b) \(AG=\dfrac{2}{3}AD\)
Bài 1: Cho tam giác ABC. Trên tia đối AB lấy điểm D sao cho ADAB. Trên cạnh AC lấy E sao cho AE 1/3AC. Tia BE cắt CD tại M. Chứng minh:
a. M là trung điểm CD b,ư. AM 1/2BC
c. Từ B kẻ BF // CE và BF CE( F thuộc nửa mặt phẳng bờ BC không chứa A). Gọi K là trung điểm BC, chứng minh E,K,F thẳng hàng
Bài 2: Cho tam giác ABC, vẽ đường trung tuyến BM. Trên tia BM lấy G và K sao cho BG 2/3BM và G là trung điểm BK. Gọi N là trung điểm KC, GN cắt CM ở O. Chứng minh;
a. O là trọng tâm ta...
Đọc tiếp
Bài 1: Cho tam giác ABC. Trên tia đối AB lấy điểm D sao cho AD=AB. Trên cạnh AC lấy E sao cho AE= 1/3AC. Tia BE cắt CD tại M. Chứng minh:
a. M là trung điểm CD b,ư. AM = 1/2BC
c. Từ B kẻ BF // CE và BF = CE( F thuộc nửa mặt phẳng bờ BC không chứa A). Gọi K là trung điểm BC, chứng minh E,K,F thẳng hàng
Bài 2: Cho tam giác ABC, vẽ đường trung tuyến BM. Trên tia BM lấy G và K sao cho BG= 2/3BM và G là trung điểm BK. Gọi N là trung điểm KC, GN cắt CM ở O. Chứng minh;
a. O là trọng tâm tam giác GKC b. GO = 1/3BC
Bài 3:Cho tam giác ABC có góc A = 120 độ. Các tia phân giác góc A và C cắt nhau ở O, cắt các cạnh BC và AB lần lượt ở D và E, Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F. Chứng minh:
a. BO vuông góc với BF b. Góc BDF = góc ADF c. 3 điểm D,E,F thẳng hàng
MONG MỌI NGƯỜI GIÚP MK NHA MẤY BÀI NÀY MK KO LÀM ĐC, MK ĐANG CẦN GẤP AI GIẢI ĐC THÌ GIÚP MK NHA. CẢM ƠN TRƯỚC NHÉ
Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng :
a) Các cạnh của tam giác BGD bằng \(\dfrac{2}{3}\) các đường trung tuyến của tam giác ABC
b) Các đường trung tuyến của tam giác BGD bằng một nửa các cạnh của tam giác ABC

