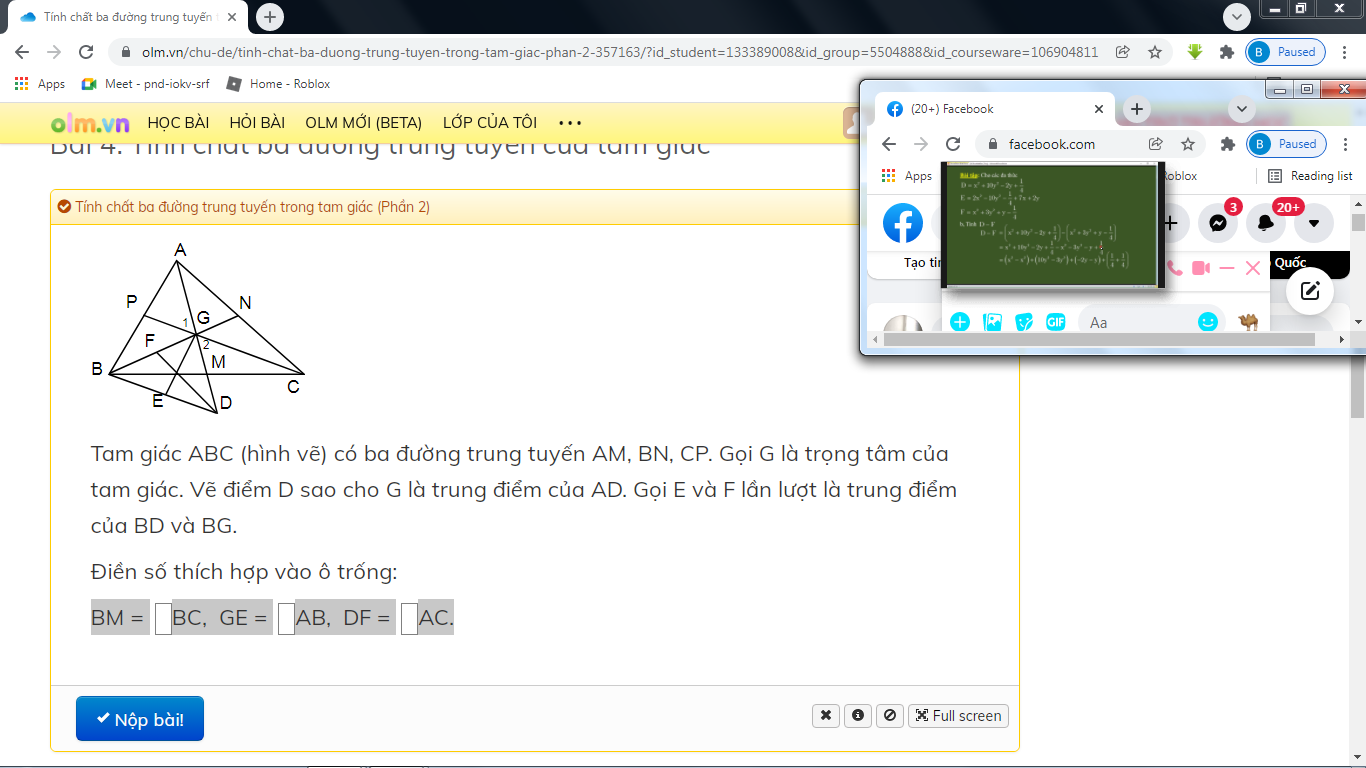
a) Gọi AM , BN , CP là các đường trung tuyến của \(\Delta ABC\) . Ta có GD = AG = 2GM và GD = GM + MD nên GM = MD
\(\Delta BMD=\Delta CMG\left(c.g.c\right)\)
\(\Rightarrow BD=CG=\dfrac{2}{3}CP\) (1)
Ta có \(BG=\dfrac{2}{3}BN\) (2)
\(GD=AG=\dfrac{2}{3}AM\) (3)
Từ (1) , (2) , (3) suy ra các cạnh của \(\Delta BGD=\dfrac{2}{3}\) các đường trung truyến của \(\Delta ABC\)
b) Gọi CE , DF là các đường trung tuyến của \(\Delta BGD\) . Từ đây tự chứng minh \(BM=\dfrac{1}{2}BC;GE=\dfrac{1}{2}AB;DF=AN=\dfrac{1}{2}AC\)