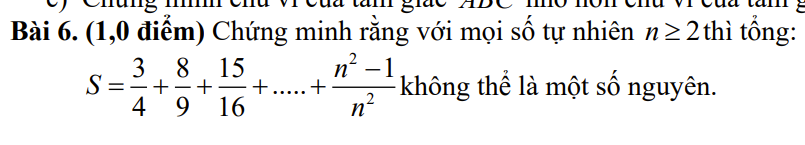Question

bài 6 chưng minh ạ

Answer 1

\(S\) có \(\left(n-1\right)\) số hạng:

\(S=\dfrac{3}{4}+\dfrac{8}{9}+\dfrac{15}{16}+...+\dfrac{n^2-1}{n^2}=\left(1-\dfrac{1}{2^2}\right)+\left(1-\dfrac{1}{3^2}\right)+\left(1-\dfrac{1}{4^2}\right)+...+\left(1-\dfrac{1}{n^2}\right)\)

\(S=n-1-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}\right)< n-1\left(1\right)\)

Mặt khác \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{\left(n-1\right).n}=1-\dfrac{1}{n}\)

\(S>n-1-1+\dfrac{1}{n}=n-2+\dfrac{1}{n}>n-2\left(2\right)\)

Từ (1) và (2) ta có: \(n-2< S< n-1\)

Vậy S không có giá trị nguyên với mọi số tự nhiên