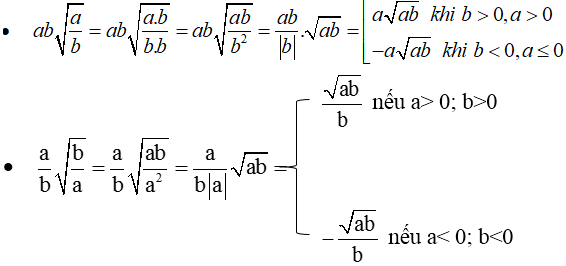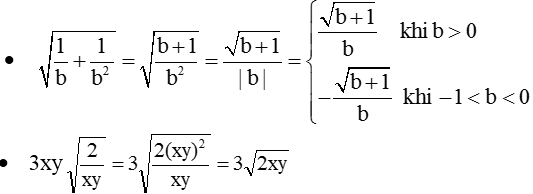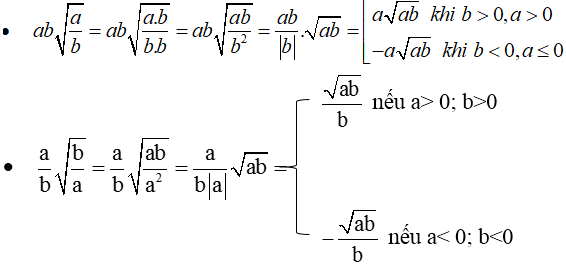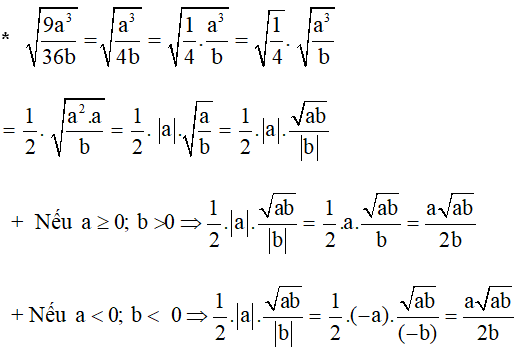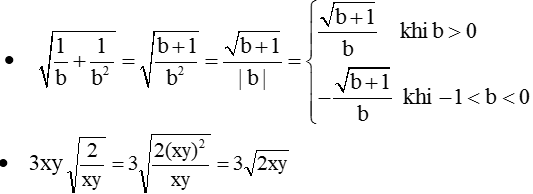Question

Bài 49 (trang 29 SGK Toán 9 Tập 1)

Khử mẫu của biểu thức lấy căn

$ab\sqrt{\dfrac{a}{b}}$ ; $\dfrac{a}{b} \sqrt{\dfrac{b}{a}}$ ; $\sqrt{\dfrac{1}{b}+\dfrac{1}{b^{2}}}$ ; $\sqrt{\dfrac{9 a^{3}}{36 b}}$ ; $3 xy \sqrt{\dfrac{2}{x y}}$.

(Giả thiết các biểu thức có nghĩa). 
 

Answer 1

(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)

#Học tốt!!!

Answer 2

\(ab\cdot\sqrt{\dfrac{a}{b}}=a\cdot\sqrt{ab}\)

\(\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}=\dfrac{\sqrt{a\cdot b}}{b}\)

\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)

\(\sqrt{\dfrac{9\cdot a^3}{36\cdot b}}=\dfrac{\sqrt{a^3\cdot b}}{2\cdot b}\)

\(3\cdot x\cdot y\cdot\sqrt{\dfrac{2}{x\cdot y}}=3\cdot\sqrt{2\cdot x\cdot y}\)

Answer 3

\(a\cdot b\cdot\sqrt{\dfrac{a}{b}}=a\cdot\sqrt{a\cdot b}\)

\(\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}=\dfrac{\sqrt{a\cdot b}}{b}\)

\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)

\(\sqrt{\dfrac{9\cdot a^3}{36\cdot b}}=\dfrac{\sqrt{a^3\cdot b}}{2\cdot b}\)

\(3\cdot x\cdot y\cdot\sqrt{\dfrac{2}{x\cdot y}}=3\cdot\sqrt{2\cdot x\cdot y}\)

Answer 4

ab=ab|b|ab

abba=a|a|⋅bab

Thu gọn kết quả hơn ta được:

-) Nếu $a>0,b>0$, ta có:

abba=abb

-) Nếu $a<0,b<0$, ta có:

abba=−abb 

1 b+1 b2=b+1| b|

9a336 b=a3 b2| b|=|a|ab2| b|=aab2 b
+) 

Answer 5

Answer 6

+) \mathrm{ab} \sqrt{\dfrac{\mathrm{a}}{\mathrm{b}}}=\dfrac{\mathrm{ab}}{|\mathrm{b}|} \sqrt{\mathrm{ab}}abba​​=∣b∣ab​ab​

+) \dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{\mathrm{a}}{|\mathrm{a}| \cdot \mathrm{b}} \sqrt{\mathrm{ab}}ba​ab​​=∣a∣⋅ba​ab​

Thu gọn kết quả hơn ta được:

-) Nếu $\mathrm{a}>0,\mathrm{b}>0$, ta có:

\dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{\sqrt{\mathrm{ab}}}{\mathrm{b}}ba​ab​​=bab​​

-) Nếu $a<0,b<0$, ta có:

\dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{-\sqrt{a b}}{b}ba​ab​​=b−ab​​ 

+) \sqrt{\dfrac{1}{\mathrm{~b}}+\dfrac{1}{\mathrm{~b}^{2}}}=\dfrac{\sqrt{\mathrm{b}+1}}{|\mathrm{~b}|} b1​+ b21​​=∣ b∣b+1​​

+) \sqrt{\dfrac{9 \mathrm{a}^{3}}{36 \mathrm{~b}}}=\dfrac{\sqrt{\mathrm{a}^{3} \mathrm{~b}}}{2|\mathrm{~b}|}=\dfrac{|\mathrm{a}| \sqrt{\mathrm{ab}}}{2|\mathrm{~b}|}=\dfrac{\mathrm{a} \sqrt{\mathrm{ab}}}{2 \mathrm{~b}}36 b9a3​​=2∣ b∣a3 b​​=2∣ b∣∣a∣ab​​=2 baab​​
+) 3 \mathrm{xy} \sqrt{\dfrac{2}{\mathrm{xy}}}=3 \mathrm{xy} \cdot \dfrac{\sqrt{2 \mathrm{xy}}}{\mathrm{xy}}=3 \sqrt{2 \mathrm{xy}}3xyxy2​​=3xy⋅xy2xy​​=32xy​

Có thể nhận xét $\mathrm{x}\mathrm{y}>0$, dùng cách đưa } nhân tử xy

Đúng 0

Bình luận (0)

 Khách vãng lai đã xóa

Answer 7

ab=aba.bb.b=ababb2=ababb2=abab|b|.

ab|b|=ababb=aab. 

ab|b|=−ababb=−aab.

+ Ta có:

abba=abb.aa.a=ababa2

ab.aba2

aabb|a|=aabab=abb.

aabb|a|=−aabab=−abb.

+ Ta có:

1b+1b2=bb2+1b2=b+1b2

b+1b2=b+1|b|.

b+1|b|=b+1b.

b+1|b|=−b+1b.

+ Ta có:

9a336b=936.a3b=14.a3.bb.b

12.a2.abb2.

2xy có nghĩa nên 

Answer 8

\(ab\sqrt{\dfrac{a}{b}}=\sqrt{a^2b^2\dfrac{a}{b}}=\sqrt{a^3b}\)

\(\dfrac{a}{b}\sqrt{\dfrac{b}{a}}=\sqrt{\dfrac{a^2}{b^2}\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{ab}}{b}\)

\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\sqrt{\dfrac{b+1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)

\(\sqrt{\dfrac{9a^3}{36b}}=\sqrt{\dfrac{a^3}{4b}}=\dfrac{a\sqrt{a}}{2\sqrt{b}}=\dfrac{a\sqrt{ab}}{2b}\)

\(3xy\sqrt{\dfrac{2}{xy}}=\sqrt{9xy^2.\dfrac{2}{xy}}=\sqrt{18xy}\)

Answer 9

+) \(ab\sqrt{\dfrac{a}{b}}=ab.\dfrac{\sqrt{a}}{\sqrt{b}}=ab.\dfrac{\sqrt{a}.\sqrt{b}}{\sqrt{b}.\sqrt{b}}=ab.\dfrac{\sqrt{ab}}{\sqrt{b^2}}=ab.\dfrac{\sqrt{ab}}{|b|}\)

\(Th1:b>0\Rightarrow ab.\dfrac{\sqrt{ab}}{b}=a\sqrt{ab}\)

\(Th2:b< 0\Rightarrow ab.\dfrac{\sqrt{ab}}{-b}=-a\sqrt{ab}\)

+)\(\dfrac{a}{b}.\sqrt{\dfrac{b}{a}}=\dfrac{a}{b}.\dfrac{\sqrt{b}}{\sqrt{a}}=\dfrac{a}{b}.\dfrac{\sqrt{b}.\sqrt{a}}{\sqrt{a^2}}=\dfrac{a}{b}.\dfrac{\sqrt{ab}}{|a|}\)

\(Th1:a>0\Rightarrow\dfrac{a}{b}.\dfrac{\sqrt{a}}{b}=\dfrac{\sqrt{ab}}{b}\)

\(Th2:a< 0\Rightarrow\dfrac{a}{b}.\dfrac{\sqrt{ab}}{\left(-a\right)}=\dfrac{-\sqrt{ab}}{b}\)

+)\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\sqrt{\dfrac{b+1}{b}}=\dfrac{\sqrt{b+1}}{\sqrt{b^2}}=\dfrac{\sqrt{b+1}}{|b|}\)

\(Th1:b>0\Rightarrow\dfrac{\sqrt{b+1}}{b}\)

\(Th2:b< 0\Rightarrow\dfrac{-\sqrt{b+1}}{b}\)

+)\(\sqrt{\dfrac{9a^3}{36b}}=\sqrt{\dfrac{a^3}{4b}}=\dfrac{\sqrt{a^2}.\sqrt{a}}{2\sqrt{b}}=\dfrac{|a|.\sqrt{a}.\sqrt{b}}{2\sqrt{b}.\sqrt{b}}=\dfrac{|a|.\sqrt{ab}}{2.|b|}\)

\(Th1:a>0,b>0\Rightarrow\dfrac{a.\sqrt{ab}}{2b}\)

\(Th2:a< 0,b< 0\Rightarrow\dfrac{-a.\sqrt{ab}}{2b}\)

+)\(3xy\sqrt{\dfrac{2}{xy}}=3xy.\dfrac{\sqrt{2}}{\sqrt{xy}}=3xy.\dfrac{\sqrt{2}}{\sqrt{xy}}.\dfrac{\sqrt{xy}}{\sqrt{xy}}=3xy.\dfrac{\sqrt{2xy}}{|xy|}\)

\(Vì\) x,y>0\(\Rightarrow3xy.\dfrac{\sqrt{2xy}}{xy}\)

Answer 10

 

 

 

 

 

Answer 11

Answer 12

\(\sqrt{a^3b}\);\(\dfrac{\sqrt{ab}}{b}\);\(\dfrac{\sqrt{b+1}}{\left|b\right|}\);\(\dfrac{\sqrt{a^3b}}{2\left|b\right|}\);\(3\sqrt{2xy}\)

Answer 13

 

Answer 14

\(3\sqrt{2xy}\)

Answer 15

+) \mathrm{ab} \sqrt{\dfrac{\mathrm{a}}{\mathrm{b}}}=\dfrac{\mathrm{ab}}{|\mathrm{b}|} \sqrt{\mathrm{ab}}abba​​=∣b∣ab​ab​

+) \dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{\mathrm{a}}{|\mathrm{a}| \cdot \mathrm{b}} \sqrt{\mathrm{ab}}ba​ab​​=∣a∣⋅ba​ab​

Thu gọn kết quả hơn ta được:

-) Nếu $\mathrm{a}>0,\mathrm{b}>0$, ta có:

\dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{\sqrt{\mathrm{ab}}}{\mathrm{b}}ba​ab​​=bab​​

-) Nếu $a<0,b<0$, ta có:

\dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{-\sqrt{a b}}{b}ba​ab​​=b−ab​​ 

+) \sqrt{\dfrac{1}{\mathrm{~b}}+\dfrac{1}{\mathrm{~b}^{2}}}=\dfrac{\sqrt{\mathrm{b}+1}}{|\mathrm{~b}|} b1​+ b21​​=∣ b∣b+1​​

+) \sqrt{\dfrac{9 \mathrm{a}^{3}}{36 \mathrm{~b}}}=\dfrac{\sqrt{\mathrm{a}^{3} \mathrm{~b}}}{2|\mathrm{~b}|}=\dfrac{|\mathrm{a}| \sqrt{\mathrm{ab}}}{2|\mathrm{~b}|}=\dfrac{\mathrm{a} \sqrt{\mathrm{ab}}}{2 \mathrm{~b}}36 b9a3​​=2∣ b∣a3 b​​=2∣ b∣

Đúng 0

Bình luận (0)

 Khách vãng lai đã xóa

Answer 16

Answer 17

Answer 18

ab=ab|b|ab

abba=a|a|⋅bab

Thu gọn kết quả hơn ta được:

-) Nếu $a>0,b>0$, ta có:

abba=abb

-) Nếu $a<0,b<0$, ta có:

abba=−abb 

1 b+1 b2=b+1| b|

9a336 b=a3 b2| b|=|a|ab2| b|=aab2 b
+) 

Answer 19

Answer 20

+) \mathrm{ab} \sqrt{\dfrac{\mathrm{a}}{\mathrm{b}}}=\dfrac{\mathrm{ab}}{|\mathrm{b}|} \sqrt{\mathrm{ab}}abba​​=∣b∣ab​ab​

+) \dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{\mathrm{a}}{|\mathrm{a}| \cdot \mathrm{b}} \sqrt{\mathrm{ab}}ba​ab​​=∣a∣⋅ba​ab​

Thu gọn kết quả hơn ta được:

-) Nếu $\mathrm{a}>0,\mathrm{b}>0$, ta có:

\dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{\sqrt{\mathrm{ab}}}{\mathrm{b}}ba​ab​​=bab​​

-) Nếu $a<0,b<0$, ta có:

\dfrac{\mathrm{a}}{\mathrm{b}} \sqrt{\dfrac{\mathrm{b}}{\mathrm{a}}}=\dfrac{-\sqrt{a b}}{b}ba​ab​​=b−ab​​ 

+) \sqrt{\dfrac{1}{\mathrm{~b}}+\dfrac{1}{\mathrm{~b}^{2}}}=\dfrac{\sqrt{\mathrm{b}+1}}{|\mathrm{~b}|} b1​+ b21​​=∣ b∣b+1​​

+) \sqrt{\dfrac{9 \mathrm{a}^{3}}{36 \mathrm{~b}}}=\dfrac{\sqrt{\mathrm{a}^{3} \mathrm{~b}}}{2|\mathrm{~b}|}=\dfrac{|\mathrm{a}| \sqrt{\mathrm{ab}}}{2|\mathrm{~b}|}=\dfrac{\mathrm{a} \sqrt{\mathrm{ab}}}{2 \mathrm{~b}}36 b9a3​​=2∣ b∣a3 b​​=2∣ b∣

Đúng 0

Bình luận (0)

 Khách vãng lai đã xóa

Answer 21

Answer 22

a\(a\sqrt{ab}\)b\(\dfrac{\sqrt{ab}}{b}\)c\(\dfrac{\sqrt{b+1}}{b}\)d\(\dfrac{\sqrt{a^3}}{2b}\)e\(\dfrac{3\sqrt{xy}}{xy}\)

Answer 23

+) $3xy\sqrt{\frac{2}{xy}}=3xy\cdot \frac{\sqrt{2xy}}{xy}=3\sqrt{2xy}$

Answer 24

 

Answer 25

Answer 26

Answer 27

 

​​=3

Answer 28

 

 

Answer 29

 

Answer 30