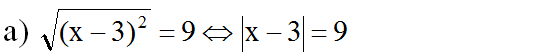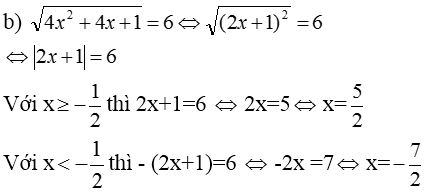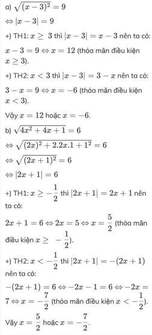a) \(\sqrt{\left(x-3\right)^2}=9\Leftrightarrow\left|x-3\right|=9\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=9\\x-3=-9\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=12\\x=-6\end{cases}}\)
Vậy ...
b) \(\sqrt{4x^2+4x+1}=6\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)
\(\Leftrightarrow\left|2x+1\right|=6\Leftrightarrow\orbr{\begin{cases}2x+1=6\\2x+1=-6\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{2}\\x=-\frac{7}{2}\end{cases}}\)
Vậy ...
a) x=12 hoặc x = -6
b) x = 5/2 hoặc x = - 7/2
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
a) \(\sqrt{\left(x-3\right)^2}=9.TH1:x-3=9\Leftrightarrow x=12;TH2:3-x=9\Leftrightarrow x=-6\)
b) \(\sqrt{4x^2+4x+1}=6\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6.TH1:2x+1=6\Leftrightarrow2x=5\Leftrightarrow x=\dfrac{5}{2};TH2:-2x-1=6\Leftrightarrow-2x=7\Leftrightarrow x=\dfrac{-7}{2}\)
\(a=-6;b=6;x=-\dfrac{7}{2}\)
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
- Với x ≥ 3 thì |x - 3| = x - 3 nên ta được:
x - 3 = 9 ⇔ x = 12
- Với x < 3 thì |x - 3| = 3 - x nên ta được:
3 - x = 9 ⇔ x = -6
Vậy phương trình có hai nghiệm: x = 12; x = -6
\(a,\sqrt{\left(x-3\right)^2}=9\)
<=>\(\left|x-3\right|=9\)
<=> \(\left[{}\begin{matrix}x-3=9\\x-3=-9\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x=12\\x=-6\end{matrix}\right.\)
Vậy x=12 hoặc x=-6
b, \(\sqrt{4x^2+4x+1}=6\)
<=>\(\sqrt{\left(2x+1\right)^2}=6\)
<=>\(\left|2x+1\right|=6\)
<=>\(\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\) <=>\(\left[{}\begin{matrix}2x=5\\2x=-7\end{matrix}\right.\) <=>\(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{-7}{2}\end{matrix}\right.\)
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
a, ⇒|x-3| =9 chia thành 2 trường hợp :\(\left[{}\begin{matrix}x-3=9\\x-3=-9\end{matrix}\right.\)
TH1: x-3 =9 TH2 : x-3= -9
⇔x = 9 +3 =12 ⇔ x = -9 +3 = -6 Vậy x =12;x= -6
b ⇒\(\sqrt{\left(2x+1\right)}^2\) = 6 ⇔|2x + 1| = 6 chia thành 2 trường hợp:\(\left[{}\begin{matrix}2x+1=6\\2x+1=-6\end{matrix}\right.\)
TH1:2x+1 =6 ⇔2x=6-1 TH2: 2x+1= -6⇔ 2x = -6 -1
⇔2x =5⇔x \(\dfrac{5}{2}\) ⇔ 2x= -7 ⇔x = \(\dfrac{-7}{2}\)
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
\(\sqrt{\left(x-3\right)^2}=9\)
\(\Leftrightarrow \left|x-3\right|=9\)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b,\(\sqrt{4x^2+4x+1}=6\)
\(\Leftrightarrow\sqrt{\left(2x\right)^2+2\cdot2x\cdot1+1^2}=6\)
\(\sqrt{\left(2x+1\right)^2}=6\)
\(\Leftrightarrow\left|2x+1\right|=6\)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy
a) [x=12; x=-6
vậy x = 12 ; x= -6
2=9
⇔ |x−3|=9
+) TH1: x≥3 thì |x−3|=x−3 nên ta có:
x−3=9 ⇔ x=12 (thỏa mãn điều kiện x≥3).
+) TH2: x<3 thì |x−3|=3−x nên ta có:
3−x=9 ⇔ x=−6 (thỏa mãn điều kiện x<3).
Vậy x=12 hoặc x=−6.
2+4x+1=6
22=6
2=6
⇔ |2x+1|=6
+) TH1: x≥−12 thì |2x+1|=2x+1 nên ta có:
2x+1=6 ⇔ 2x=5 ⇔ x=52 (thỏa mãn điều kiện x≥−12).
+) TH2: x<−12 thì |2x+1|=−(2x+1) nên ta có:
−(2x+1)=6 ⇔ −2x−1=6 ⇔ −2x=7 ⇔ x=−72 (thỏa mãn điều kiện x<−12).
Vậy x=52 hoặc x=−72.
a,x=12 x=-6
b,\(\dfrac{-7}{2}\)
a)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
(thỏa mãn điều kiện ).
Vậy hoặc .
b)
+) TH1: thì nên ta có:
(thỏa mãn điều kiện ).
+) TH2: thì nên ta có:
a)\(\sqrt{\left(x-3\right)^2}\) = 9 ⇔ \(\left|x-3\right|\) = 9
+ TH1 : x ≥ 0 thì \(\left|x-3\right|\) = x - 3 nên ta có :
x - 3 = 9 ⇔ x = 12
+ TH2 : x < 0 thì \(\left|x-3\right|\) = 3 - x nên ta có :
3 - x = 9 ⇔ x = -6
vậy x = 12 hoặc x = -6
b) \(\sqrt{4x^2+4x+1}\) = 6
⇔ \(\sqrt{\left(2x\right)^2+2\cdot2x\cdot1+1^2}\) = 6
⇔ \(\sqrt{\left(2x+1\right)^2}\) = 6
⇔ \(\left|2x+1\right|\) = 6
+ TH1 : x ≥ \(-\dfrac{1}{2}\) thì \(\left|2x+1\right|\) = 2x + 1 nên ta có :
2x + 1 = 6 ⇔ 2x = 5 ⇔ x = \(\dfrac{5}{2}\)
+ TH2 : x < \(-\dfrac{1}{2}\) thì \(\left|2x+1\right|\) = -(2x + 1) nên ta có :
-(2x + 1) = 6 ⇔ -2x -1 = 6 ⇔ -2x = 7 ⇔ x = \(-\dfrac{7}{2}\)
vậy x = \(\dfrac{5}{2}\) hoặc x = \(-\dfrac{7}{2}\)
- Với x ≥ 3 thì |x - 3| = x - 3 nên ta được:
x - 3 = 9 ⇔ x = 12
- Với x < 3 thì |x - 3| = 3 - x nên ta được:
3 - x = 9 ⇔ x = -6
Vậy phương trình có hai nghiệm: x = 12; x = -6
a)\(\sqrt{\left(x-3\right)^2}=9\) \(\Leftrightarrow\left|x-3\right|=9\) \(\Leftrightarrow x-3=9\Leftrightarrow x=12\) vay x=12. b)\(\sqrt{4x^2+4x+1}=6\)
\(\Leftrightarrow\left|2x+1\right|=6\) \(\Leftrightarrow x=\dfrac{5}{2}\)vay x=\(\dfrac{5}{2}\)
Câu a; \(x_1=12\) ;\(x_2=-6\) Câu b;\(x_1=\dfrac{5}{2};x_2=-\dfrac{7}{2}\)
Các câu hỏi tương tự
Bài 35 (trang 20 SGK Toán 9 Tập 1)
Tìm $x$, biết:
a) $\sqrt{(x-3)^2}=9$ ; b) $\sqrt{4x^2+4x+1}=6$.
Bài 35 (trang 20 SGK Toán 9 Tập 1)
Tìm $x$, biết:
a) $\sqrt{(x-3)^2}=9$ ; b) $\sqrt{4x^2+4x+1}=6$.
Bài 35 (trang 20 SGK Toán 9 Tập 1)
Tìm $x$, biết:
a) $\sqrt{(x-3)^2}=9$ ; b) $\sqrt{4x^2+4x+1}=6$.
Bài 36 (trang 20 SGK Toán 9 Tập 1)
Mỗi khẳng định sau đúng hay sai? Vì sao?
a) $0,01 = \sqrt{0,0001}$ ;
b) $-0,5 = \sqrt{-0,25}$ ;
c) $\sqrt{39} < 7$ và $\sqrt{39} > 6$ ;
d) $(4 -\sqrt{3}).2x < \sqrt{3}(4 - \sqrt{13})$
$\Leftrightarrow$ $2x < \sqrt{13}$.
Bài 31 (trang 19 SGK Toán 9 Tập 1)
a) So sánh $\sqrt{25-16}$ và $\sqrt{25}-\sqrt{16}$ ;
b) Chứng minh rằng, với $a>b>0$ thì $\sqrt{a}-\sqrt{b}<\sqrt{a-b}$.
Bài 30 (trang 19 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $\dfrac{y}{x}.\sqrt{\dfrac{x^2}{y^4}}$ với $x>0,y \ne 0$ ; b) $2y^2.\sqrt{\dfrac{x^4}{4y^2}}$ với $y<0$ ;
c) $5xy.\sqrt{\dfrac{25x^2}{y^6}}$ với $x<0$,$y>0$; d) $0,2x^3y^3.\sqrt{\dfrac{16}{x^4y^8}}$ với $x \ne 0, y\ne 0$.
Bài 29 (trang 19 SGK Toán 9 Tập 1)
Tính
a) $\dfrac{\sqrt{2}}{\sqrt{18}}$ ; b) $\dfrac{\sqrt{15}}{\sqrt{735}}$ ;
c) $\dfrac{\sqrt{12500}}{\sqrt{500}}$ ; d) $\dfrac{\sqrt{6^5}}{\sqrt{2^3.3^5}}$.
Bài 28 (trang 18 SGK Toán 9 Tập 1)
Tính
a) $\sqrt{\dfrac{289}{25}}$ ; b) $\sqrt{2\dfrac{14}{25}}$ ;
c) $\sqrt{\dfrac{0,25}{9}}$ ; d) $\sqrt{\dfrac{8,1}{16}}$.
Bài 34 (trang 19 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $ab^2.\sqrt{\dfrac{3}{a^2b^4}}$ với $a<0$,$b \ne 0$ ; b) $\sqrt{\dfrac{27(a-3)^2}{48}}$ với $a>3$ ;
c) $\sqrt{\dfrac{9+12a+4a^2}{b^2}}$ với $a \ge -1,5$ và $b<0$ ; d) $(a-b).\sqrt{\dfrac{ab}{(a-b)^2}}$ với $a<b<0$.