Bài 3 : Một xưởng sản xuất hai loại sản phâm .Mỗi kg sản phẩm loại 1 cần 3kg nguyên liệu và 20 giờ làm việc đem lại mức lời 40000 đồng .Mỗi kg sản phẩm loại 2 cần 2kg nguyên liệu và 20 giờ làm việc đem lại mức lời 30000 đồng .Xưởng có 150kg nguyên liệu và 1200 giờ làm việc .Nên sản xuất mỗi loại sản phẩm bao nhiêu kg để có mức lợi nhuận cao nhất
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 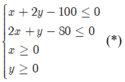
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0
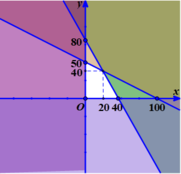
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.

