Bạn ghi rõ ràng ra chứ ghi mỗi thế này thì ai biết ở chỗ bài nào? tuyen tran tuyen tran
bài 20 :
Lời giải:
a) Cặp góc đồng vị khác là: ∠(P3) = ∠(Q3) = 30o(lưu ý :∠ là góc nha bạn)
b) Cặp góc so le trong là: ∠(P3) = ∠(Q1) = 30o
c) ∠(P3) và ∠(Q2) là hai góc trong cùng phía.
∠(P3) = 30o; ∠(Q2) = 150o.
d) ∠(P1) và ∠(Q4) là hai góc ngoài cùng phía
∠(P1) = 30o; ∠(Q4) = 150o.
bài 4.2 :
Lời giải:
∠D2 = 39° vì là góc đồng vị với ∠E = 39°.
∠D4 = 39° vì là góc đối đỉnh với ∠D2.
∠D3 = 141° vì bù với góc ∠D4.
∠D1 = 141° vì là góc đối đỉnh với ∠D3.
bài 4.3
Lời giải:
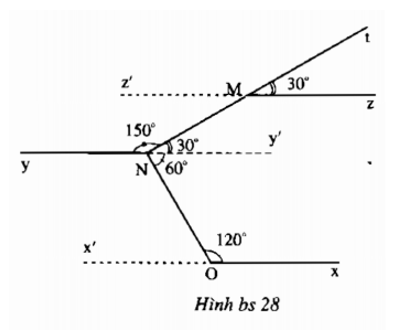
a) Vẽ Ny’ là tia đối của tia Ny, Mz’ là tia đối của tia Mz. Khi đó, góc MNy’ bề bù với góc Mny, do đó ∠MNy' = 30°. Từ đó, z’Mz song song với yNy’ vì có một cặp góc đồng vị bằng nhau (cùng bằng 30°).
b) Vì ∠MNO = 90° và ∠MNy' = 30° suy ra ∠ONy' = 60°. Vẽ Ox’ là tia đối của tia Ox. Khi đó, góc NOx’ kề bù với góc Nox, do đó ∠NOx' = 60°. Từ đó, x’Ox song song với yNy’ vì có một cặp góc đồng vị bằng nhau (cùng bằng 60°).
bài 5.2:Lời giải:
Trong trường hợp hình d) thì a và b không song song với nhau vì tổng hai góc trong cùng phía không bằng 180°.
bài 5.1Lời giải:
Các kết quả trên đều đúng
bài 31
Giải
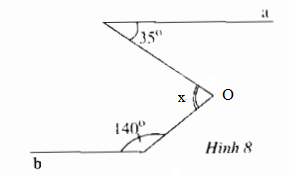
Qua O kẻ đường thẳng c // a
Vì a // b nên c // b
ˆA=ˆO1A^=O1^ (hai góc so le trong)
Mà ˆA=35∘A^=35∘ nên ˆO1=35∘O1^=35∘
Vì ˆO2O2^ và ˆBB^ là hai góc trong cùng phía của hai đường thẳng song song nên ˆO2+ˆB=180∘O2^+B^=180∘
⇒ˆO2=180∘−ˆB⇒ˆO2=180∘−140∘=40∘x=ˆAOB=ˆO1+ˆO2=35∘+40∘=75∘
bài 6.1:
Lời giải:
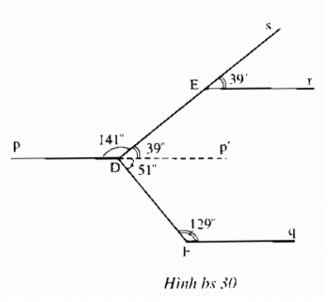
Thấy ngay hai đường thẳng DE và DF cắt nhau tại D.
Kẻ thêm Dp’ là tia đối của tia Dp.
Khi đó Er song song với pDp’ nên ∠EDp' = 39° (vì là góc đồng vị với ∠E).
Lại do pDp’ song song với Fq nên ∠FDp' = 51° (vì là góc trong cùng phía với ∠F)
Từ đó ∠EDF = ∠EDp' + ∠p'DF = 39° + 51° = 90°.
Vậy hai đường thẳng DE và DF vuông góc với nhau.
bài 41
Lời giải:
a. Hình vẽ:
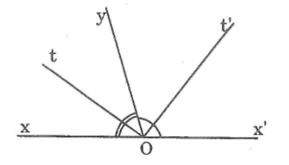
b.

c. Chứng minh:
1) ∠tOy = 1/2. ∠xOy = 1/2. mo (Vì Ot là tia phân giác của )
2) ∠x'Oy = 180o - ∠xOy = 180o - mo (Vì ∠x'Oy và ∠xOy kề bù)
3) ⇒ ∠t'Oy = 1/2. ∠x'Oy = 1/2. (180o - mo) (Vì Ot’ là phân giác của ∠x'Oy)
4) ⇒ ∠tOt' = ∠tOy + ∠t'Oy = 1/2. mo + 1/2. (180o - mo) = 90o.
Kết luận: Vậy hai tia phân giác của hai góc kề bù tạo thành góc vuông.
bài 42
Lời giải:
Chứng minh:
∠(IDM) =∠(IDN) (vì DI là tia phân giác của ∠(MDN) (1)
∠(IDM) =∠(EDK) (vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra ∠(EDK) =∠(IDN) (điều phải chứng minh)
bài 48
Lời giải:
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy.
Ta có: ∠(B2 ) +∠(xAB) =180o
(hai góc trong cùng phía)
Mà ∠(xAB) =140o(gt)
Suy ra: ∠(B2 ) =180-∠(xAB) =180o-140o=40o
Mà: ∠(B1 ) +∠(B2 ) =∠(ABC) (B1 ) =∠(ABC) -(B2 ) =70o-40o=30o (1)
∠(yCB) +∠(BCy') =180o(2 góc kề bù)
∠BCy'=180o-∠(yCB) =180o-150o=30o (2)
Từ (1) và (2) ta có: ∠(B1 ) =∠(BCy')
Suy ra: Cy’ // Bz ( vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra Ax // Cy
bài 49
Kẻ Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ∠A +∠(B2 ) =180o
(2 góc trong cùng phía) (1)
∠A +∠B +C =360o (gt)
∠A +∠(B2 ) +∠(B1 ) +∠C =360o (2)
Từ (1)và (2)suy ra :
∠(B1) +∠C =180o
∠(C1 ) +∠∠C =180o (hai góc kề bù) (4)
Từ (3) và (4) suy ra: ∠(B1 ) =∠(C1 )
Suy ra: Cy’ // Bz (vì có cặp góc so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra Ax //Cy
bài I.3

Đó là SBT
bài 46
a)
- Vẽ đoạn thẳng AC=3cmAC=3cm
- Trên cùng một nửa mặt phẳng bờ ACAC vẽ cung tròn tâm AA bán kính 4cm4cm và cung tròn tâm CC có bán kính 4cm.4cm.
- Hai cung tròn trên cắt nhau tại B.B.
- Vẽ các đoạn AB,BCAB,BC ta được tam giác ABCABC cần dựng.
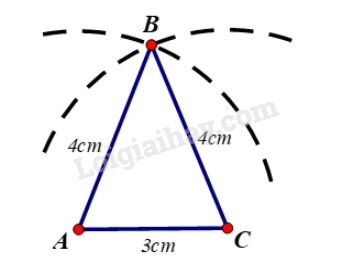
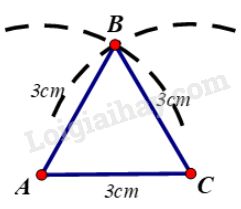
b) Vẽ đoạn thẳng AC=3cmAC=3cm
- Trên cùng một nửa mặt phẳng bờ ACAC vẽ cung tròn tâm AA bán kính 3cm3cm và cung tròn tâm CC bán kính 3cm3cm.
- Hai cung tròn trên cắt nhau tại BB.
- Vẽ các đoạn thẳng AB,BCAB,BC ta được tam giác ABCABC cần dựng.
bài 47
Hình 116
Ta có: ΔABD∆ABD cân tại AA vì có AB=AD.AB=AD.
ΔACE∆ACE cân tại AA vì AC=AEAC=AE (do AB=AD,BC=DEAB=AD,BC=DE nên AB+BC=AD+DEAB+BC=AD+DE hay AC=AEAC=AE).
Hình 117
Ta tính được
ˆG=180o−(ˆH+ˆI)G^=180o−(H^+I^)=1800−(700+400)=700=1800−(700+400)=700
Do đó ΔGHI∆GHI cân tại II vì ˆG=ˆH=700G^=H^=700
Hình 118
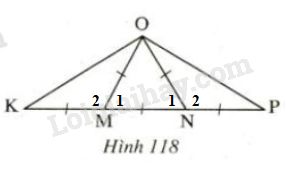
ΔOMK∆OMK là tam giác cân tại MM vì OM=MKOM=MK
ΔONP∆ONP là tam giác cân tại NN vì ON=NPON=NP
ΔOMN∆OMN là tam giác đều vì OM=MN=ONOM=MN=ON
Do đó: ˆM1=ˆN1=600M1^=N1^=600 (1)
ˆM1+ˆM2=1800M1^+M2^=1800 (hai góc kề bù) (2)
ˆN1+ˆN2=1800N1^+N2^=1800 (hai góc kề bù) (3)
Từ (1), (2) và (3) suy ra: ˆM2=ˆN2M2^=N2^
Xét ΔOMK∆OMK và ΔONP∆ONP có:
+) OM=ONOM=ON (gt)
+) MK=NPMK=NP (gt)
+) ˆM2=ˆN2M2^=N2^ (chứng minh trên)
⇒ΔOMK=ΔONP⇒∆OMK=∆ONP (c.g.c)
⇒ˆMKO=ˆNPO⇒MKO^=NPO^ (hai góc tương ứng)
Vậy ΔOKP∆OKP là tam giác cân tại O.O.
bài 53
Lời giải chi tiết
a) Vẽ
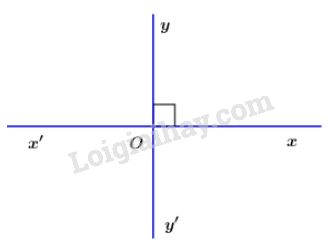
b)
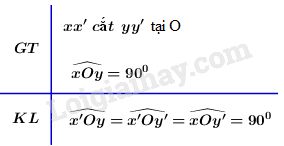
c)
1) ˆxOy+ˆx′Oy=180oxOy^+x′Oy^=180o (vì là hai góc kề bù).
2) 90o+ˆx′Oy=180o90o+x′Oy^=180o (theo giả thiết và căn cứ vào 1).
3) ˆx′Oy=90ox′Oy^=90o (căn cứ vào 2).
4) ˆx′Oy′=ˆxOyx′Oy′^=xOy^ (vì là hai góc đối đỉnh).
5) ˆx′Oy′=90ox′Oy′^=90o (căn cứ vào 4 và giả thiết).
6) ˆy′Ox=ˆx′Oyy′Ox^=x′Oy^ (vì là hai góc đối đỉnh).
7) ˆy′Ox=90oy′Ox^=90o (căn cứ vào 6 và 3).
d) Trình bày lại cách chứng minh một cách gọn hơn.
Ta có: ˆxOy+ˆx′Oy=180oxOy^+x′Oy^=180o (hai góc kề bù)
Mà ˆxOy=90oxOy^=90o (gt) nên 90o+ˆx′Oy=180o90o+x′Oy^=180o
⇒ˆx′Oy=180o−90o=90o⇒x′Oy^=180o−90o=90o
ˆx′Oy=ˆxOy′x′Oy^=xOy′^ (hai góc đối đỉnh).
⇒ˆy′Ox=90o⇒y′Ox^=90o
ˆx′Oy′=ˆxOyx′Oy′^=xOy^ (hai góc đối đỉnh).
⇒ˆx′Oy′=90o
BÀI 52
Lời giải chi tiết
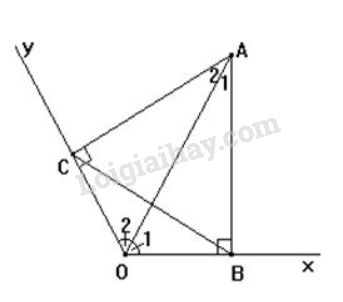
Tam giác ACOACO vuông tại CC.
Tam giác ABOABO vuông tại BB
Xét hai tam giác vuông ACOACO và ABOABO có:
+) ˆO1=ˆO2O1^=O2^ (Vì OAOA là tia phân giác góc xOyxOy)
+) AOAO chung
⇒ΔACO=ΔABO⇒∆ACO=∆ABO (cạnh huyền-góc nhọn)
⇒AC=AB⇒AC=AB (hai cạnh tương ứng)
⇒ˆA1=ˆA2⇒A1^=A2^ (hai góc tương ứng)
ˆO1=12ˆxOy=12.1200=600O1^=12xOy^=12.1200=600 (Vì OAOA là tia phân giác góc xOyxOy)
Áp dụng định lí tổng ba góc của một tam giác vào ΔOBAΔOBA ta có:
ˆO1+ˆB+ˆA1=1800⇒ˆA1=1800−ˆO1−ˆB=1800−600−900=300O1^+B^+A1^=1800⇒A1^=1800−O1^−B^=1800−600−900=300
Do đó: ˆA1=ˆA2=300A1^=A2^=300
Hay ˆBAC=ˆA1+ˆA2=600BAC^=A1^+A2^=600
Vây ΔABC∆ABC có AC=ABAC=AB và ˆBAC=600BAC^=600 nên là tam giác đều
BÀI 57
Lời giải chi tiết
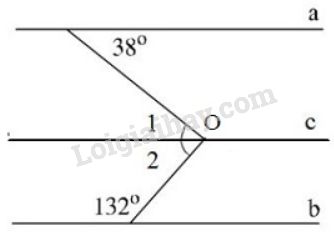
Vẽ đường thẳng c//ac//a đi qua OO (hình vẽ). Do đó a//c//ba//c//b
Vì a//ca//c nên ˆO1=38oO^1=38o (hai góc so le trong)
Vì c//bc//b nên ˆO2+132o=180oO2^+132o=180o (hai góc trong cùng phía)
⇒ˆO2=180o−132o=48o⇒O2^=180o−132o=48o
Do đó: ˆO=ˆO1+ˆO2=38o+48o=86oO^=O^1+O^2=38o+48o=86o
Vậy x=86o
BÀI 58
Lời giải chi tiết
Ta có: a⊥c,b⊥ca⊥c,b⊥c
Theo định lí : hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau. Do đó a//ba//b
⇒x+115o=180o⇒x+115o=180o (vì hai góc ở vị trí trong cùng phía)
⇒x=180o–115o=65o⇒x=180o–115o=65o
Vậy x=65o
BÀI 59
Lời giải chi tiết
+) Vì d′//d′′d′//d″ có: ˆE1E1^ và góc 60o60o là hai góc so le trong nên ˆE1=60oE1^=60o
+) Vì d′//d′′d′//d″ có: ˆG2G2^ và góc 110o110o là hai góc đồng vị nên ˆG2=110oG2^=110o
+) ˆG2+ˆG3=180oG2^+G^3=180o (hai góc kề bù)
⇒ˆG3=180o−ˆG2=180o−110o=70o⇒G3^=180o−G2^=180o−110o=70o
+) ˆD4=110oD4^=110o (vì hai góc đối đỉnh)
+) Vì d//d′d//d′ nên ˆA1=60oA1^=60o (vì hai góc đồng vị)
Ta có: ˆA5=ˆA1=60oA5^=A1^=60o (vì hai góc đối đỉnh) .
+ ˆB6=ˆB2B6^=B2^ (vì hai góc đối đỉnh)
Có ˆB2+110o=180oB2^+110o=180o (hai góc trong cùng phía)
⇒ˆB2=180o−110o=70o⇒B2^=180o−110o=70o.
Do đó: ˆB6=70oB6^=70o.
Vậy ˆE1=60o,ˆG2=110o,ˆG3=70o,E1^=60o,G2^=110o,G3^=70o,ˆD4=110o,ˆA5=60o,ˆB6=70o
(LƯU Ý : o LÀ ĐỘ)
CHÚC BẠN HỌC TỐT
TICK NHA