Bài 2: Hai đường thẳng vuông góc

1. Thế nào là hai đường thẳng vuông góc?

Định nghĩa:

Hai đường thẳng \(xx'\), \(yy'\) cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc và được kí hiệu là \(xx'\perp yy'\).

Hình vẽ:

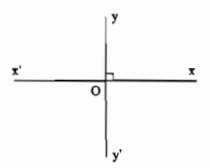
Chú ý: Khi \(xx'\) và \(yy'\) là hai đường thẳng vuông góc (và cắt nhau tại \(O\)) ta nói: Đường thẳng \(xx'\) vuông góc với đường thẳng \(yy'\) (tại \(O\)) hay đường thẳng \(yy'\) vuông góc với đường thẳng \(xx'\) (tại \(O\)) hay hai đường thẳng \(xx'\), \(yy'\)vuông góc với nhau tại \(O\).

2. Vẽ hai đường thẳng vuông góc

Ta thừa nhận tính chất sau:

Có một và chỉ một đường thẳng \(a'\) đi qua điểm \(O\) và vuông góc với dường thẳng \(a\) cho trước.

3. Đường trung trực của đoạn thẳng

Cho hình vẽ sau:

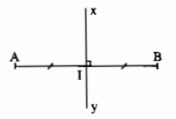
Ta thấy: 

\(I\) là trung điểm của đoạn thẳng \(AB\).

Đường thẳng \(xy\) vuông góc với đoạn thẳng \(AB\) (hay đường thẳng \(AB\)) tại \(I\).

Ta nói: Đường thẳng \(xy\) là đường trung trực của đoạn thẳng \(AB\).

Định nghĩa:

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là trung trực của đoạn thẳng đó.

Khi \(xy\) là đường trung trực của đoạn thẳng \(AB\) ta cũng nói: Hai điểm \(A\) và \(B\) đối xứng với nhau qua đường thẳng \(xy\).