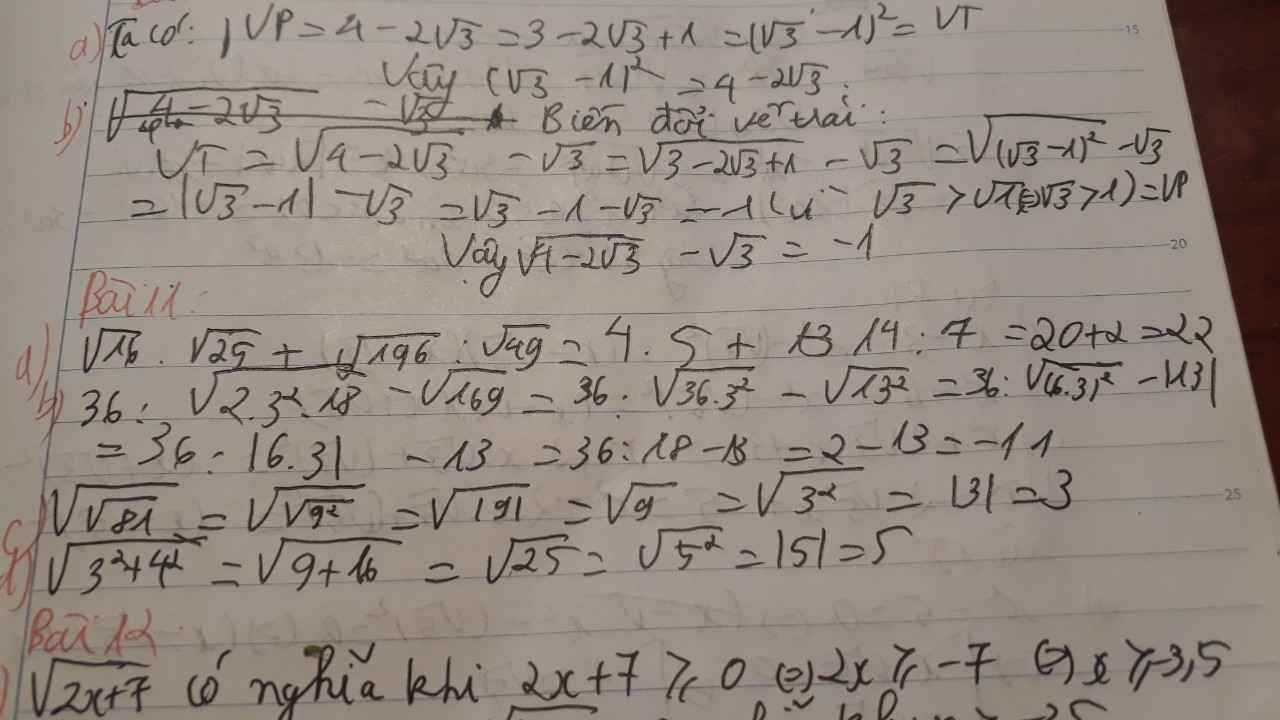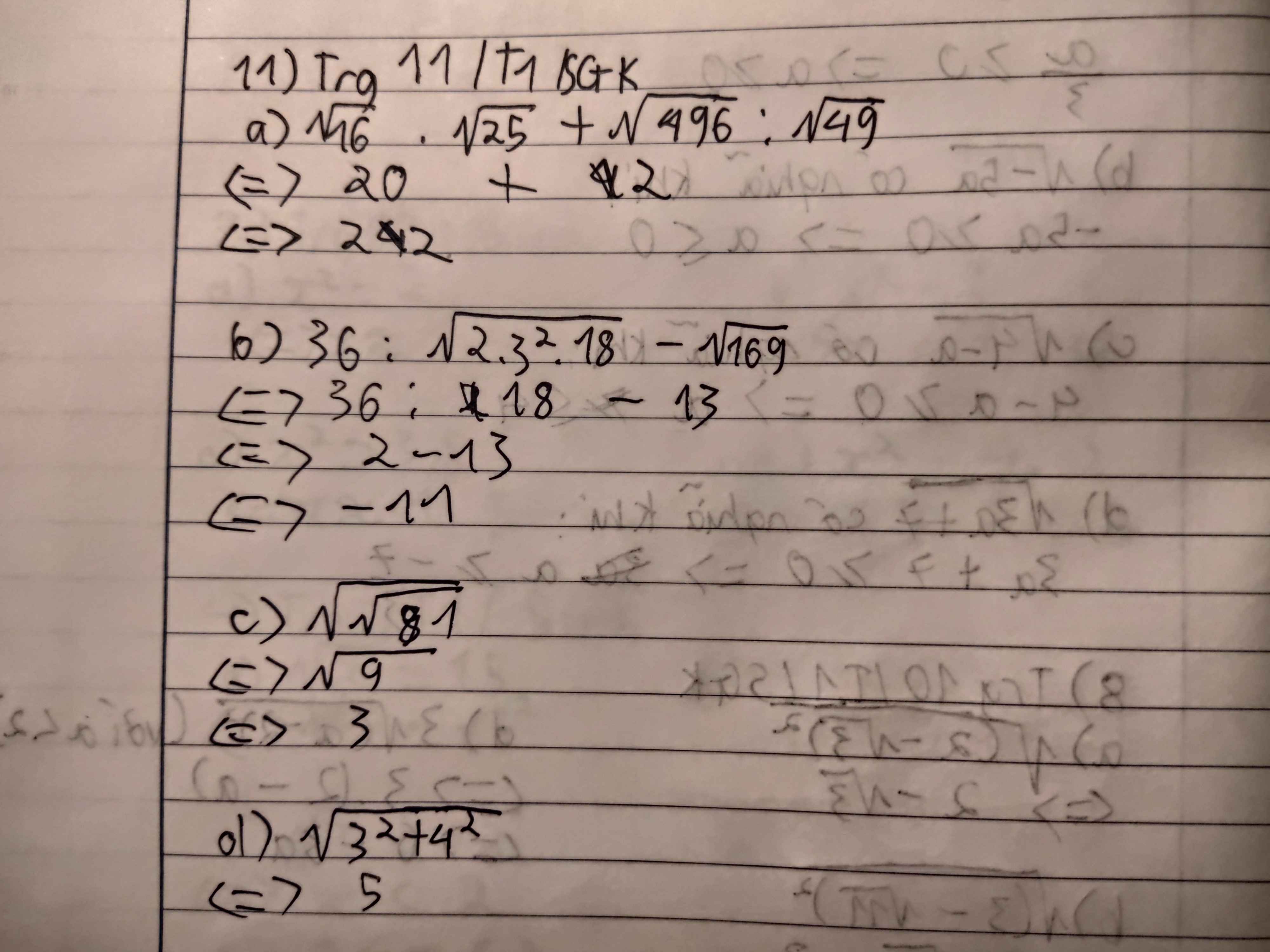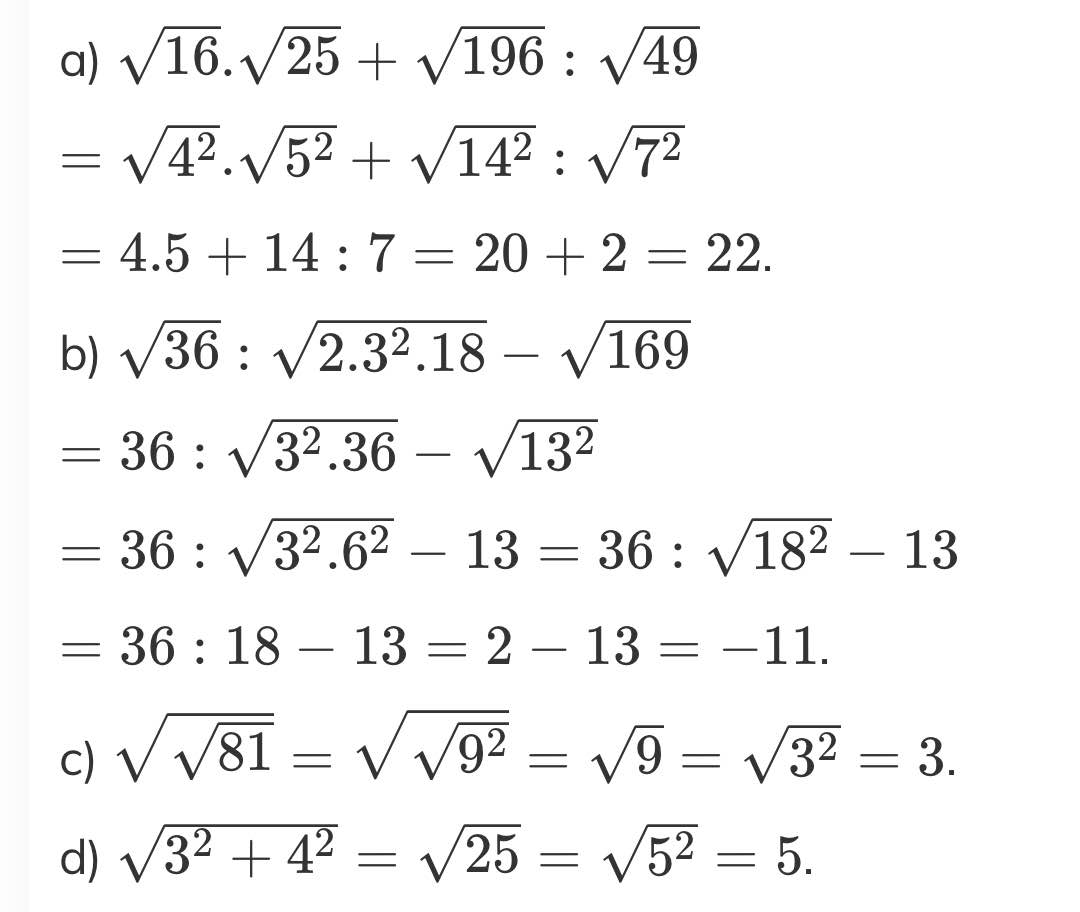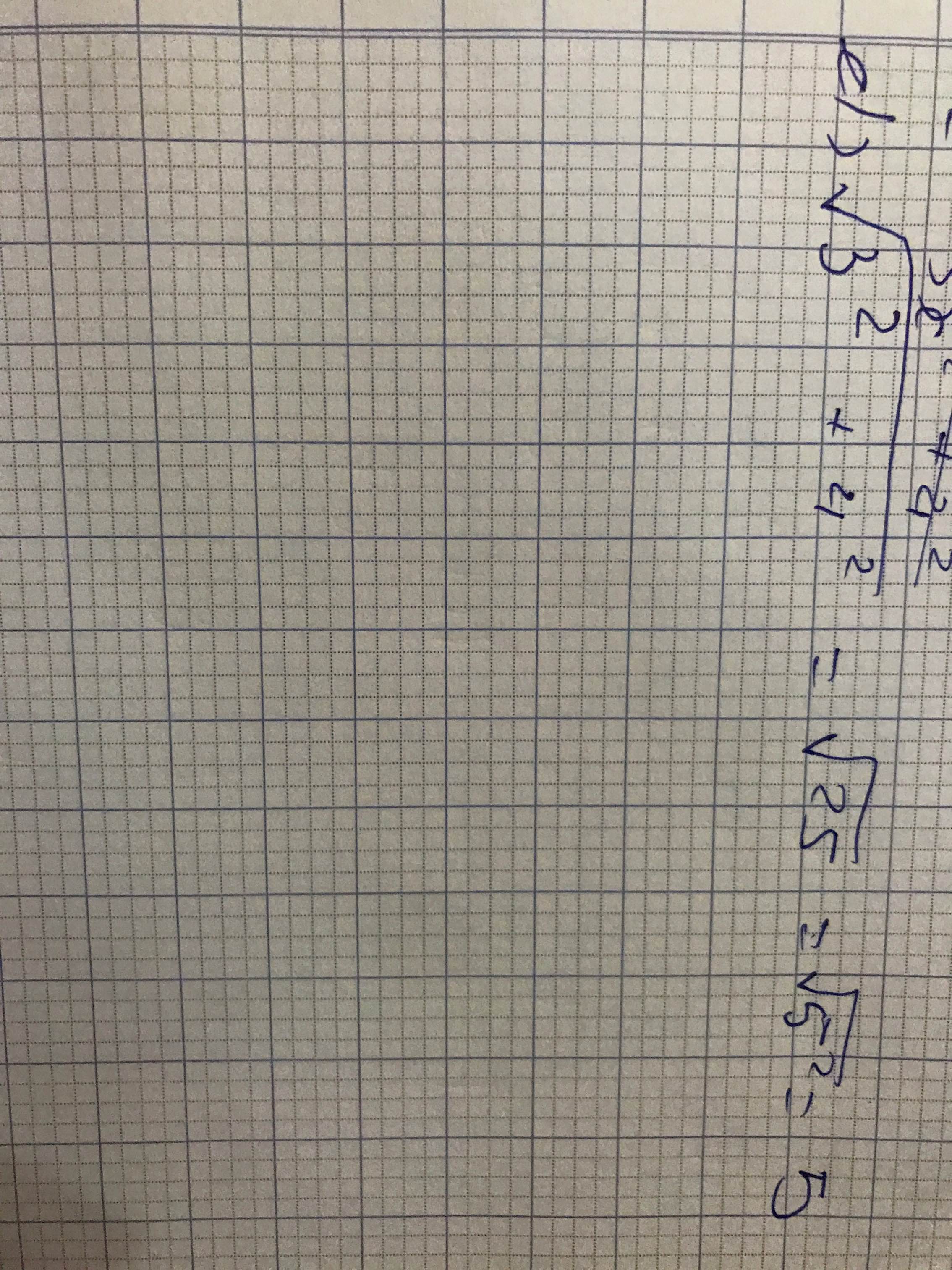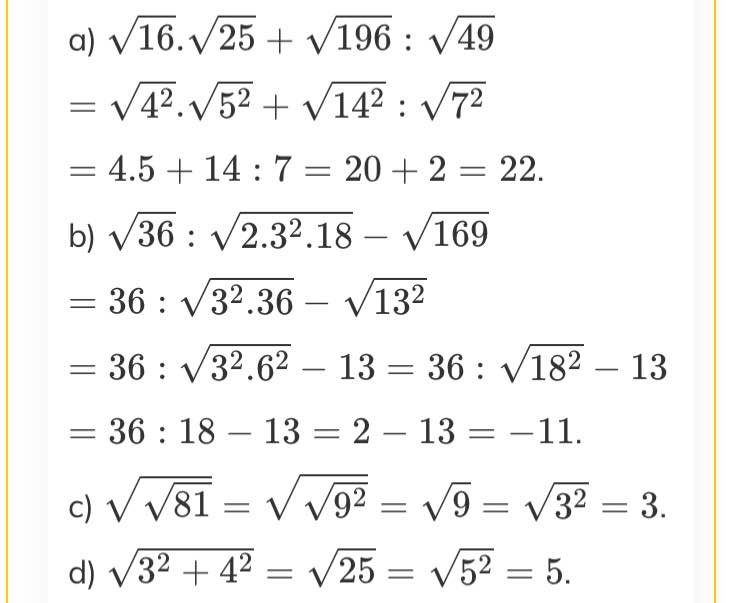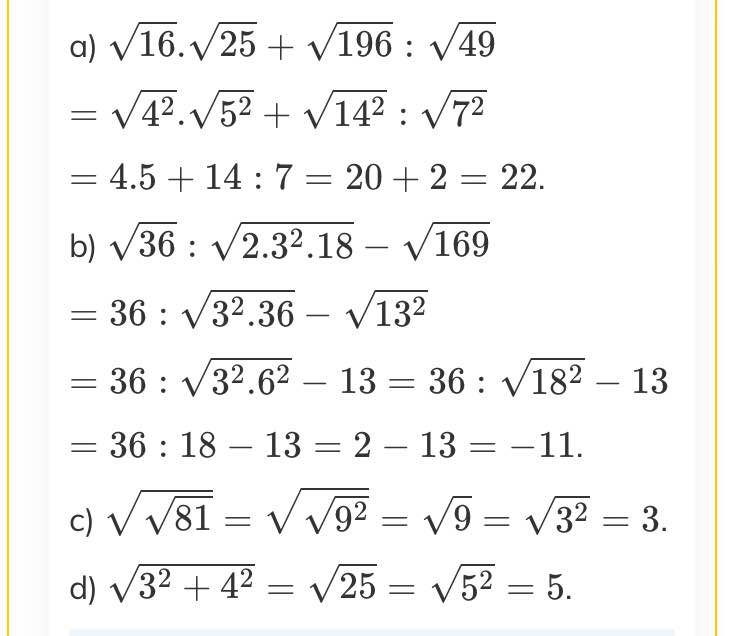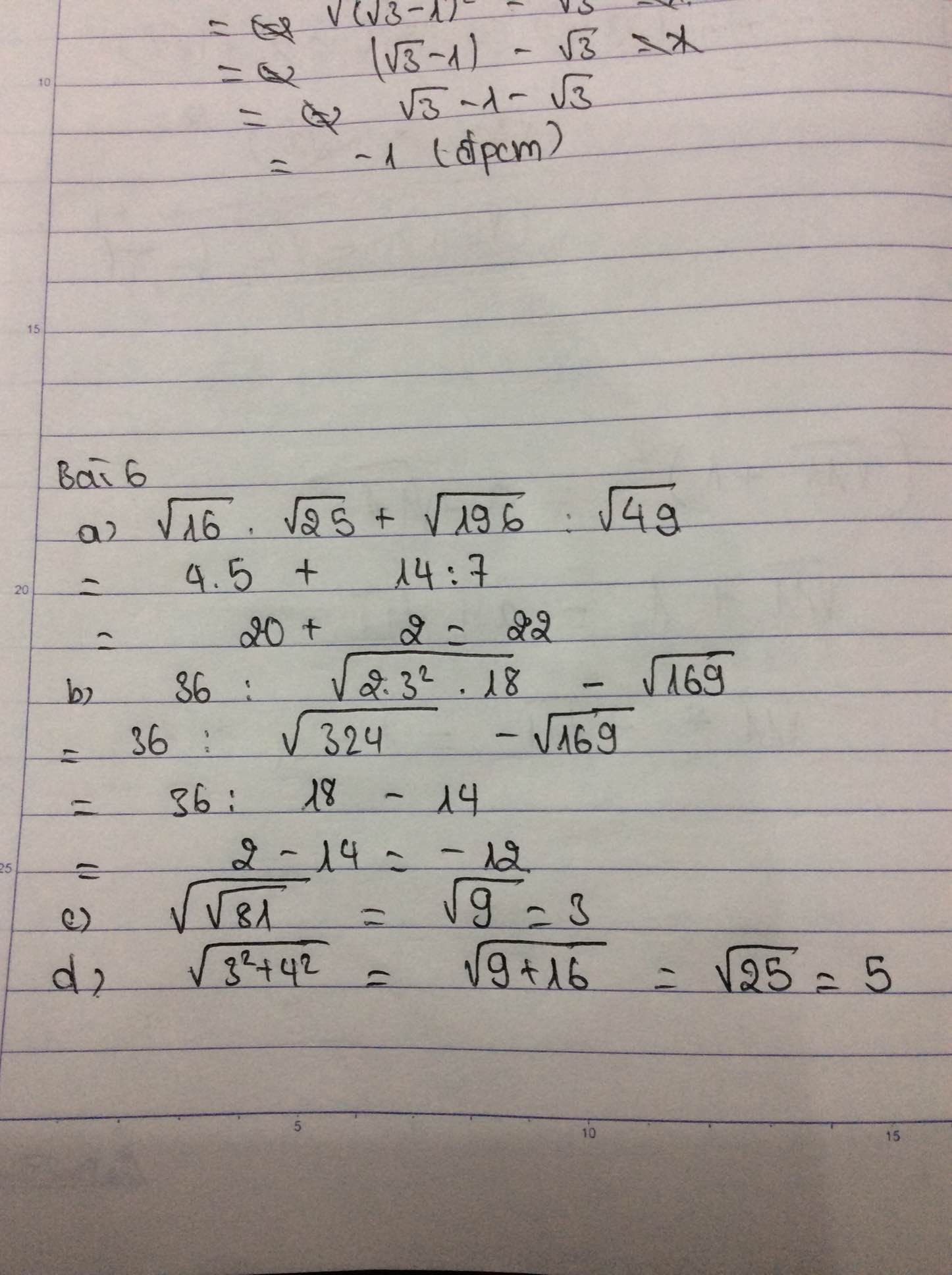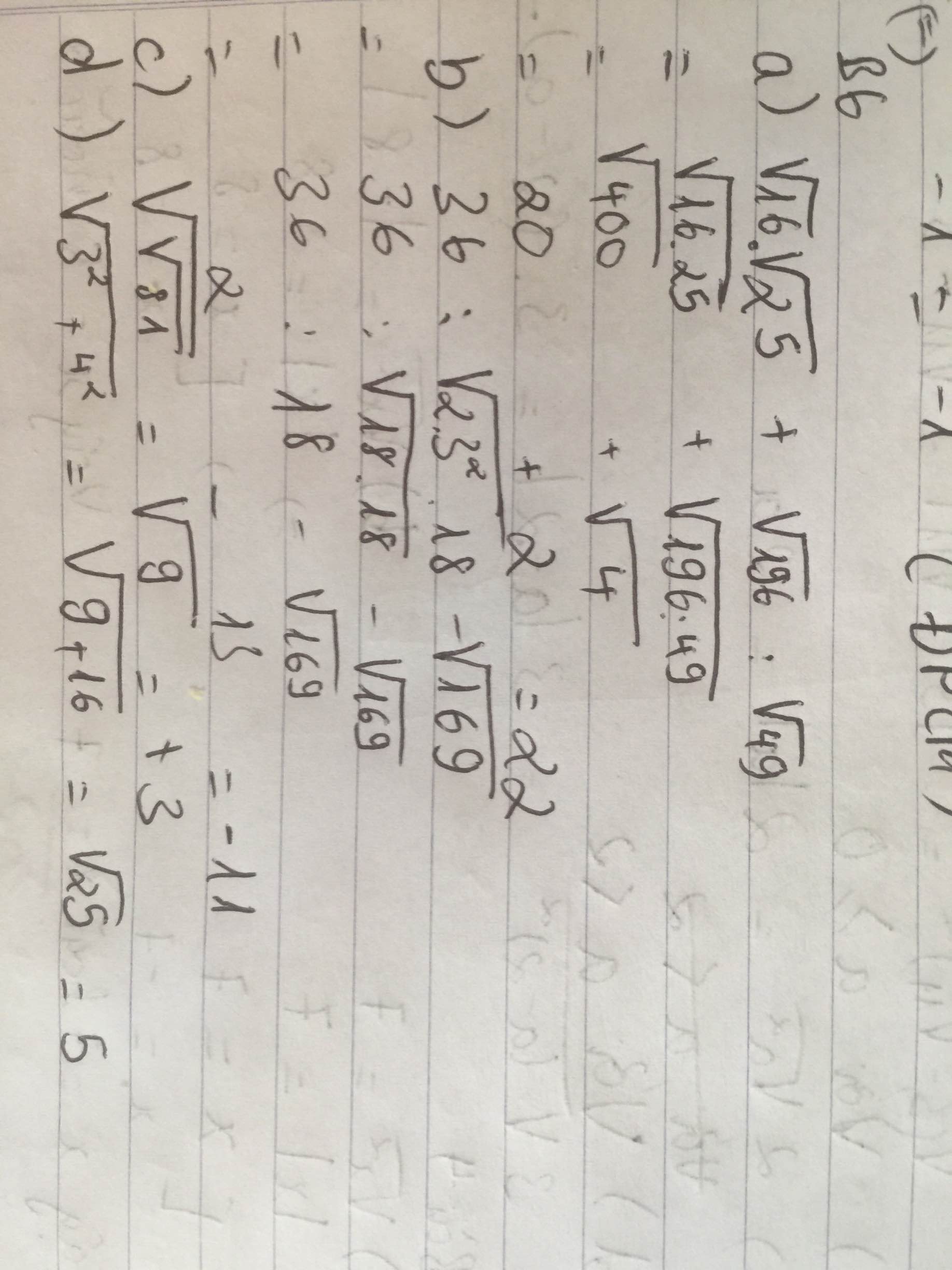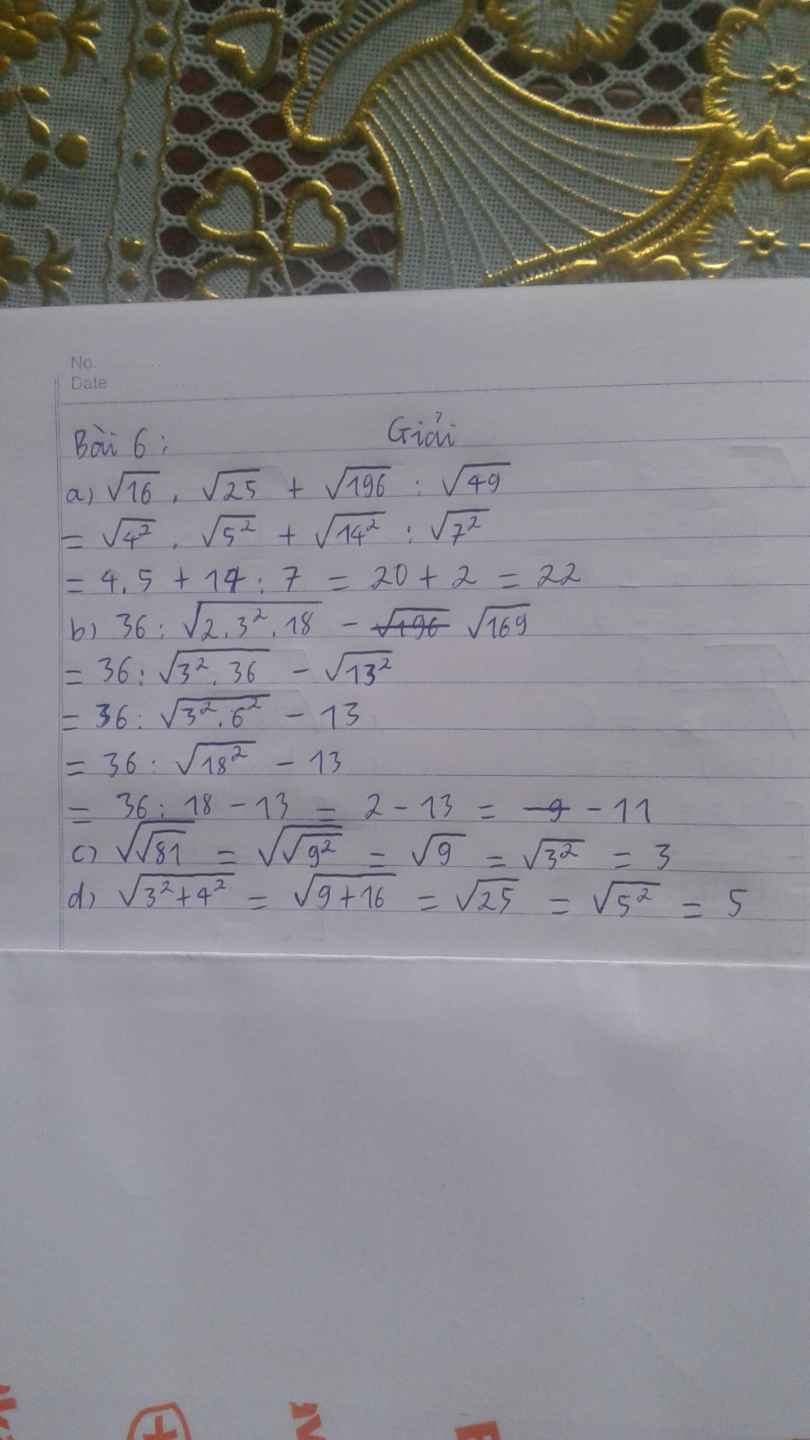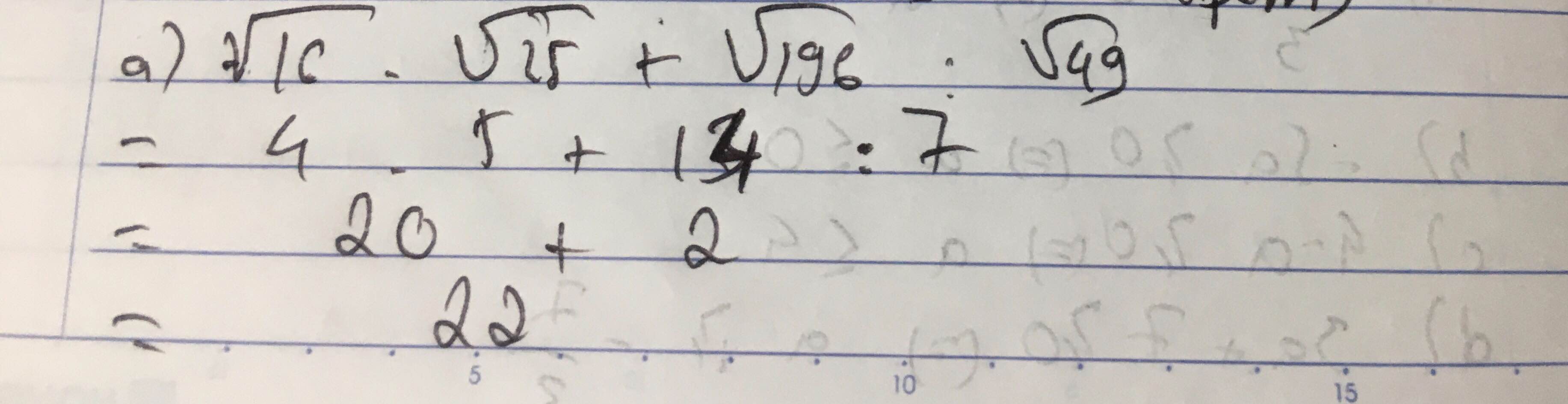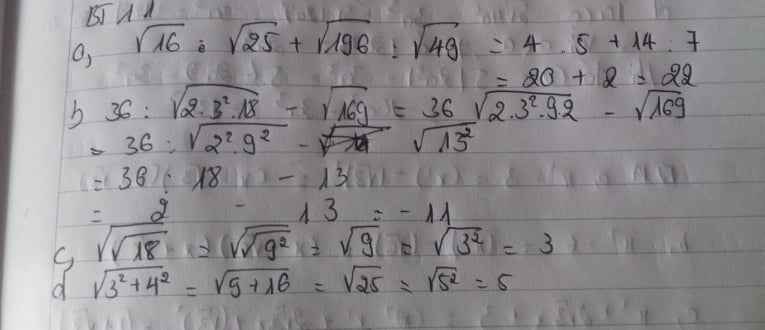a) \(\sqrt{16}\).\(\sqrt{25}\)+\(\sqrt{196}\):\(\sqrt{49}\)
=4.5+14/7
=20+2
=22
a) \(\sqrt{16}\).\(\sqrt{25}\) + \(\sqrt{196}\) : \(\sqrt{49}\) = 4.5+14:9=22
b) 36:\(\sqrt{2.3^2.18}\) - \(\sqrt{169}\)= 36 : \(\)18 - 13 = -11
c) \(\sqrt{\sqrt{81}}\) = 3
d) \(\sqrt{3^2+4^2}\)= \(\sqrt{25}\)=5
a, 4.5+ 14:7= 20+2= 22
b, 36: √2.9.18 - 13 = 36:18 -13 =-11
c, √9 = 3
d, √9+16 = √25 = 5
a) \(\sqrt{16}\times\sqrt{25}+\sqrt{196}\div\sqrt{49}=4\times5+14\div7=20+2=22\)
b) \(36\div\sqrt{2\times3^2\times18}-\sqrt{169}=36\div18-13=2-13=-11\)
c) \(\sqrt{\sqrt{81}}=3\)
d) \(\sqrt{3^2+4^2}=5\)
a.22
b.-11
c.3
d.5
a. \(\sqrt{16}\) . \(\sqrt{25}\) + \(\sqrt{196}\) : \(\sqrt{49}\)
= \(\sqrt{4^2}\) . \(\sqrt{5^2}\) + \(\sqrt{14^2}\) : \(\sqrt{7^2}\)
= 4.5 + 14:7 = 20+2=22
b. \(\sqrt{36}\) : \(\sqrt{2.3^2.18}\) - \(\sqrt{169}\)
= 36 : \(\sqrt{3^2.36}\) - \(\sqrt{13^2}\)
= 36 : 18 - 13 = 2-13 = -11
c.\(\sqrt{\sqrt{81}}\) = \(\sqrt{\sqrt{9^2}}\) = \(\sqrt{9}\) = \(\sqrt{3^2}\) = 3
d. \(\sqrt{3^2+4^2}\) = \(\sqrt{25}\) = \(\sqrt{5^2}\) = 5
a) = 4.5 + 14 : 7 = 20 + 2 = 22
b) 36 : 18 - 13 = 2 - 13 = - 11
c) \(\sqrt{9}\) = 3
d) \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5
a) \(\sqrt{4^2}.\sqrt{5^2}+\sqrt{14^2}:\sqrt{7^2}\) = \(|4|.|5|+|14|:|7|\) = 4.5+14:7 = 20+2 = 22
b) 36:\(\sqrt{2.9.2.9}-\sqrt{169}\) = 36:\(\sqrt{4}.\sqrt{9}.\sqrt{9}-\sqrt{169}\) = 2.3.3-13 = 18-3 = 15
c)\(\sqrt{\sqrt{9.9}}\) = \(\sqrt{\sqrt{9}.\sqrt{9}}\) = \(\sqrt{3.3}\) = \(\sqrt{9}\) = 3
d)\(\sqrt{9+16}=\sqrt{25}=5\)
a) \(\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49}\) = \(\sqrt{4^2}.\sqrt{5^2}+\sqrt{14^2}:\sqrt{7^2}\) = \(\left|4\right|.\left|5\right|+\left|14\right|.\left|7\right|\) = 4.5 + 14.7 =20 + 2 = 22
b)
.
b)
.
c)
a) \(\sqrt{16}.\sqrt{25}\) + \(\sqrt{169}:\sqrt{49}\)
= \(\sqrt{4^2}\).\(\sqrt{5^2}\) + \(\sqrt{14^2}:\sqrt{7^2}\)
= 4.5 + 14 : 7
= 20 + 2 = 22
b) \(\sqrt{36}:\sqrt{2.3^2.18}-\sqrt{169}\)
= 36 : \(\sqrt{3^2.36}-\sqrt{13^2}\)
= 36 : \(\sqrt{3^2.6^2}-13\)
= 36 : \(\sqrt{18^2}-13\)
= 36 : 18 - 13 = 2 - 13 = -11
c) \(\sqrt{\sqrt{81}}=\sqrt{\sqrt{9^2}}=\sqrt{9}=\sqrt{3^2}=3\)
d) \(\sqrt{3^2+4^2}=\sqrt{25}=\sqrt{5^2}=5\)
\(a,\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49}=4.5+14:7=20+2=22\)
b,\(36:\sqrt{2.3^2.18}-\sqrt{169}=36:\sqrt{324}-13=36:18-13=2-13=-11\)
c, \(\sqrt{\sqrt{81}}=3\)
d, \(\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5\)
Các câu hỏi tương tự
Bài 10 (trang 11 SGK Toán 9 Tập 1)
Chứng minh:
a) $(\sqrt{3}-1)^2=4-2\sqrt{3}$ ; b) $\sqrt{4-2\sqrt{3}}-\sqrt{3}=-1$.
Bài 7 (trang 10 SGK Toán 9 Tập 1)
Tính:
a) $\sqrt{(0,1)^2}$ ; b) $\sqrt{(-0,3)^2}$ ; c) $-\sqrt{(-1,3)^2}$ ; d) $-0,4\sqrt{(-0,4)^2}$.
Bài 9 (trang 11 SGK Toán 9 Tập 1)
Tìm x biết:
a) $\sqrt{x^2}=7$ ; b) $\sqrt{x^2}=|-8|$ ;
c) $\sqrt{4x^2}=6$ ; d) $\sqrt{9x^2}=|-12|$.
Bài 6 (trang 10 SGK Toán 9 Tập 1)
Với giá trị nào của $a$ thì mỗi căn thức sau có nghĩa:
a)$\sqrt{\dfrac{a}{3}}$; b)$\sqrt{-5a}$; c)$\sqrt{4-a}$; d)$\sqrt{3a+7}$ ?
Bài 12 (trang 11 SGK Toán 9 Tập 1)
Tìm x để mỗi căn thức sau có nghĩa:
a) $\sqrt{2x+7}$ ; b) $\sqrt{-3x+4}$ ; c) $\sqrt{\dfrac{1}{-1+x}}$ ; d) $\sqrt{1+x^2}$.
Bài 13 (trang 11 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $2\sqrt{a^2}-5a$ với $a<0$ ; b) $\sqrt{25a^2}+3a$ với $a \le 0$;
c) $\sqrt{9a^4}+3a^2$ ; d) $5\sqrt{4a^6}-3a^3$ với $a<0$.
Bài 14 (trang 11 SGK Toán 9 Tập 1)
Phân tích thành nhân tử:
a) $x^2-3$ ; b) $x^2-6$ ;
c) $x^2+2\sqrt{3}x+3$ ; d) $x^2-2\sqrt{5}x+5$.
Hướng dẫn: Dùng kết quả:
Với $a \ge 0$ thì $a = (\sqrt{a})^2$.
Bài 15 (trang 11 SGK Toán 9 Tập 1)
Giải các phương trình sau:
a) $x^2-5=0$ ; b) $x^2-2\sqrt{11}x+11=0$.
Bài 16 (trang 12 SGK Toán 9 Tập 1)
Đố. Hãy tìm chỗ sai trong phép chứng minh "Con muỗi nặng bằng con voi" dưới đây.
Giả sử con muỗi nặng $m(gam)$, còn con voi nặng $V (gam)$. Ta có:
$m^2 + V^2 = V^2 + m^2$
Cộng cả hai vế với $-2mV$, ta có:
$m^2 – 2mV + V^2 = V^2 – 2mV + m^2$
hay $(m - V)^2 = (V - m)^2$.
Lấy căn bậc hai mỗi vế của đẳng thức trên, ta được:
$\sqrt{(m - V)^2} = \sqrt{(V - m)^2}$
Do đó $m-V = V-m$
Từ đó ta có $2m = 2V$, suy ra $m = V$. Vậy con muỗi nặng bằng con voi (!).