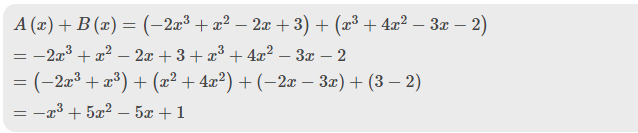\(A\left(x\right)+B\left(x\right)=\left(2x^3+x^2-2x+3\right)+\left(x^3+4x^2-3x-2\right)\)
\(A\left(x\right)+B\left(x\right)=2x^3+x^2-2x+3+x^3+4x^2-3x-2\)
\(A\left(x\right)+B\left(x\right)=\left(2x^3+x^3\right)+\left(x^2+4x^2\right)+\left(-2x-3x\right)+\left(3-2\right)\)
\(A\left(x\right)+B\left(x\right)=3x^3+5x^2-5x+1\)
`A(x)+B(x)= -2x^3 +x^2 - 2x +3 +x^3 +4x^2 -3x -2`
`A(x) +B(x) = (x^3 +2x^3 ) +(x^2 +4x^2)+(-3x-2x)+(3-2)`
`A(x)+B(x) = 3x^3 +5x^2 -5x+1`
Vậy `A(x)+B(x) = 3x^3 +5x^2 -5x+1`