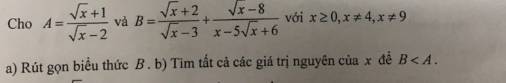Question

Anh chị nào giúp em với ạ!!

Answer 1

Lời giải:
a.

\(B=\frac{\sqrt{x}+2}{\sqrt{x}-3}+\frac{\sqrt{x}-8}{(\sqrt{x}-2)(\sqrt{x}-3)}\\ =\frac{(\sqrt{x}+2)(\sqrt{x}-2)}{(\sqrt{x}-3)(\sqrt{x}-2)}+\frac{\sqrt{x}-8}{(\sqrt{x}-2)(\sqrt{x}-3)}\\ =\frac{x-4+\sqrt{x}-8}{(\sqrt{x}-2)(\sqrt{x}-3)}=\frac{x+\sqrt{x}-12}{(\sqrt{x}-2)(\sqrt{x}-3)}\\ =\frac{(\sqrt{x}-3)(\sqrt{x}+4)}{(\sqrt{x}-2)(\sqrt{x}-3)}=\frac{\sqrt{x}+4}{\sqrt{x}-2}\)

b.

$B< A$

$\Leftrightarrow \frac{\sqrt{x}+4}{\sqrt{x}-2}< \frac{\sqrt{x}+1}{\sqrt{x}-2}$

$\Leftrightarrow \frac{\sqrt{x}+4}{\sqrt{x}-2}- \frac{\sqrt{x}+1}{\sqrt{x}-2}<0$

$\Leftrightarrow \frac{3}{\sqrt{x}-2}<0$

$\Leftrightarrow \sqrt{x}-2<0$

$\Leftrightarrow 0\leq x< 4$

Kết hợp đkxđ suy ra $0\leq x< 4$