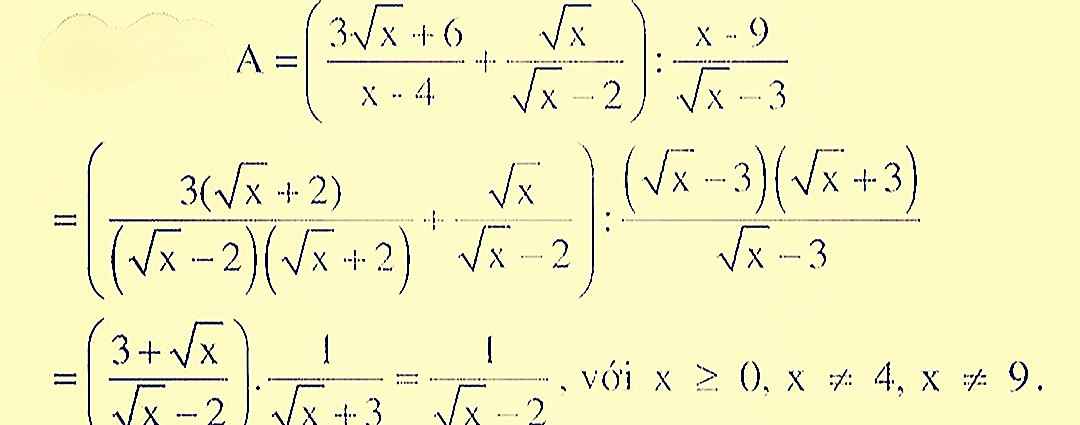Question

\(A=\left(\dfrac{3\sqrt{x}+6}{x-4}+\dfrac{\sqrt{x}}{\sqrt{x}-2}\right):\dfrac{x-9}{\sqrt{x}-3}\)

Answer 1

đk x >= 0 ; x khác 4;9 

\(A=\left(\dfrac{3\sqrt{x}+6}{x-4}+\dfrac{\sqrt{x}}{\sqrt{x}-2}\right):\dfrac{x-9}{\sqrt{x}-3}\)

\(=\left(\dfrac{3+\sqrt{x}}{\sqrt{x}-2}\right):\left(\sqrt{x}+3\right)=\dfrac{1}{\sqrt{x}-2}\)

Answer 2

Với \(x\ge0;x\ne9\):

\(A=\left(\dfrac{3\sqrt{x}+6}{x-4}+\dfrac{\sqrt{x}}{\sqrt{x}-2}\right):\dfrac{x-9}{\sqrt{x}-3}\\ =\left[\dfrac{3\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\sqrt{x}-2}\right]\cdot\dfrac{\sqrt{x}-3}{x-9}\\ =\left(\dfrac{3}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-2}\)

#$\mathtt{Toru}$

Answer 3