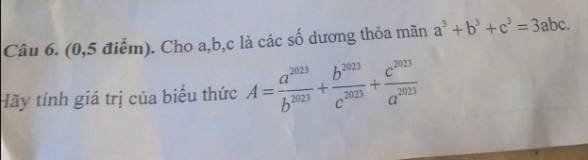Vì x,y,z>0 nên áp dung bất đẳng thức Cô-si ta có:
\(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^3}{x^2+y^2+z^2+2xy+2yz+2xz}\)
mà x+y+z=1 ⇔ x2+y2+z2+2xy+2yz+2zx=1 (bình phương cả 2 vế)
nên \(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^2}{\left(x+y+z\right)^2}\)=9
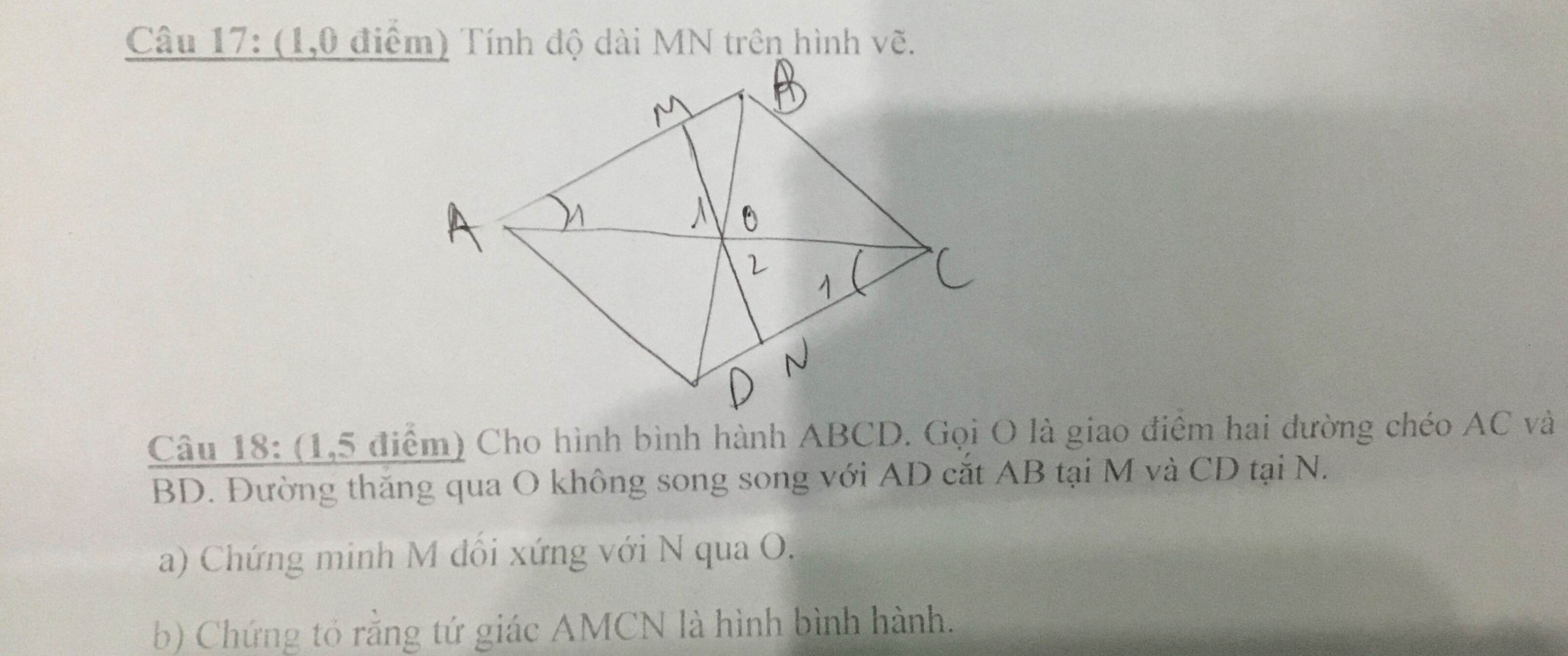
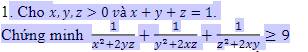 ai làm hộ em với em cần gấp;-;
ai làm hộ em với em cần gấp;-;
 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp