\(4,=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}\right)^2-9}=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}=\dfrac{3\sqrt{3}-3\sqrt{2}+9}{2+\sqrt{6}}\\ =\dfrac{\left(3\sqrt{3}-3\sqrt{2}+9\right)\left(\sqrt{6}-2\right)}{2}\\ =\dfrac{9\sqrt{2}-6\sqrt{3}-6\sqrt{3}+6\sqrt{2}+9\sqrt{6}-18}{2}\\ =\dfrac{15\sqrt{2}-12\sqrt{3}+9\sqrt{6}-18}{2}\)
\(c,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=4\Leftrightarrow x-1=16\Leftrightarrow x=17\left(tm\right)\\ d,ĐK:x\ge-5\\ PT\Leftrightarrow\sqrt{x+5}=5\Leftrightarrow x+5=25\Leftrightarrow x=20\left(tm\right)\\ e,ĐK:x\ge0\\ PT\Leftrightarrow-2\sqrt{x}=-6\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ f,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)
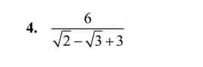
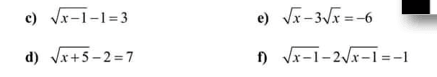









 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!