`a,`
Có `AB////CD(g t)`
`=>{(hat(A_1)=hat(ADC)(Sol etrong)),(hat(B_1)=hat(BCD)(Sol etrong)):}`
Mà `hat(ADC)=hat(BCD)` (Tứ giác `ABCD` là hình thang cân)
Nên `hat(A_1)=hat(B_1)`
`=>Delta OAB` cân tại `O(dpcm)`
`b,`
Tứ giác `ABCD` là hình thang cân `(g t)`
`=>hat(BAD)=hat(ABC);AD=BC`
Xét `Delta ABD` và `Delta BAC` có :
`{:(AB-chung),(hat(BAD)=hat(BAC)(cmt)),(AD=BC(cmt)):}}`
`=>Delta ABD=Delta BAC(c.g.c)(dpcm)`
`c,`
Có `Delta ABD=Delta BAC(cmt)`
`=>hat(D_1)=hat(C_1)` (2 góc tương ứng)
mà `hat(ADC)=hat(BCD)(cmt)`
Nên `hat(ADC)-hat(D_1)=hat(BCD)-hat(C_1)`
hay `hat(D_2)=hat(C_2)`
`=>Delta EDC` cân tại `E`
`=>ED=EC(dpcm)`
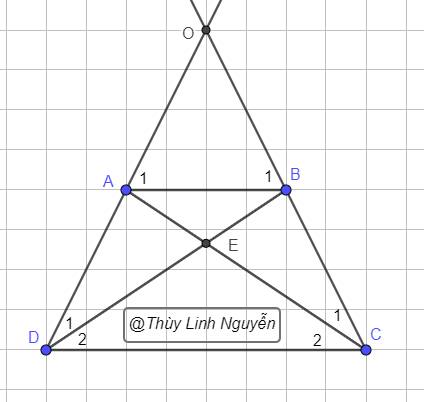
Hình:
Đúng 0
Bình luận (0)


