Lời giải:
$\overrightarrow{MA}=(1-x, 3-y), \overrightarrow{MB}=(4-x, 2-y)$
Để $MAB$ là tam giác vuông cân tại $M$ thì:
\(\left\{\begin{matrix}
\overrightarrow{MA}.\overrightarrow{MB}=0\\
MA^2=MB^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
(1-x)(4-x)+(3-y)(2-y)=0\\
(1-x)^2+(3-y)^2=(4-x)^2+(2-y)^2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x^2-5x+y^2-5y+10=0\\ 6x-2y-10=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^2-5x+y^2-5y+10=0\\ y=3x-5\end{matrix}\right.\)
\(\Leftrightarrow (x,y)=(2,1), (3,4)\)





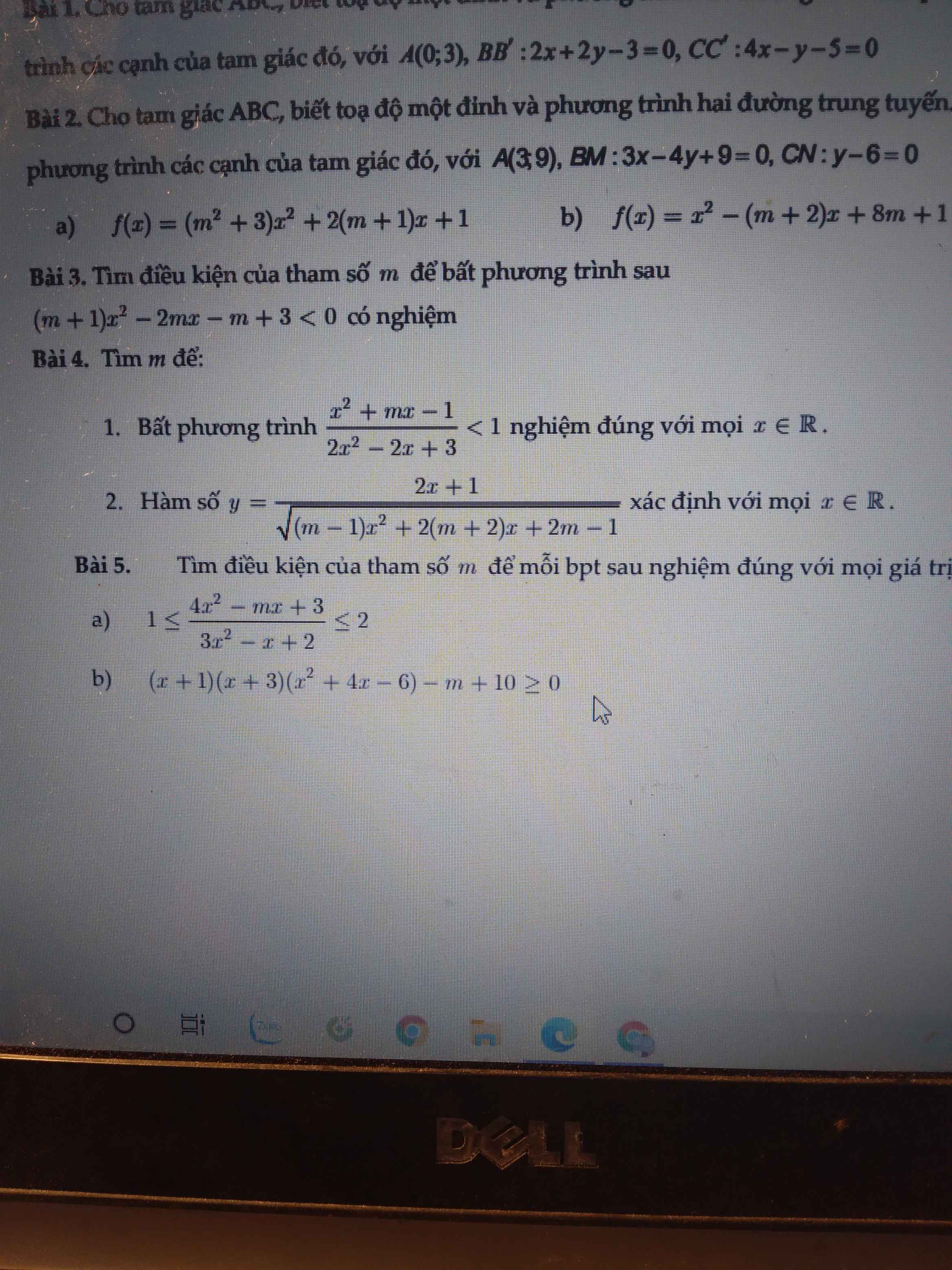
 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn