\(B=\left(\dfrac{x\sqrt{x}+x+\sqrt{x}}{x\sqrt{x}-1}-\dfrac{\sqrt{x}+3}{1-\sqrt{x}}\right).\left(\dfrac{x-1}{2x+\sqrt{x}-1}\right)\left(ĐKXĐ:x>0;x\ne1\right)\)\(=\left[\dfrac{\sqrt{x}\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\right].\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+2x-1}\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\right).\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+2x-1}\)
\(=\dfrac{2\sqrt{x}+3}{\sqrt{x}-1}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+2x-1}\)
\(=\dfrac{\left(2\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+2x-1}\)
\(=\dfrac{2x+5\sqrt{x}+3}{\sqrt{x}+2x-1}\)
Vậy \(B=\dfrac{2x+5\sqrt{x}+3}{\sqrt{x}+2x-1}\) với \(x>0;x\ne1\)
Để \(B< 0\) thì \(\dfrac{2x+5\sqrt{x}+3}{\sqrt{x}+2x-1}< 0\)
\(\Rightarrow2x+5\sqrt{x}+3< \sqrt{x}+2x-1\)
\(\Leftrightarrow4\sqrt{x}< -4\Leftrightarrow\sqrt{x}< -1\Leftrightarrow x< 1\)
Vậy \(0< x< 1\) thì \(B< 0\)
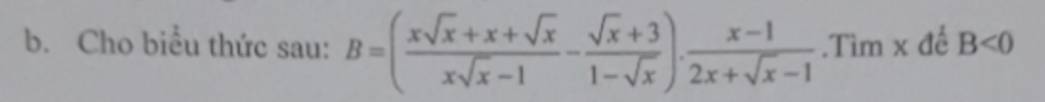 ae giúp tớ với
ae giúp tớ với 






 Giải giúp tớ với ạ, tớ cần gấp lắm
Giải giúp tớ với ạ, tớ cần gấp lắm