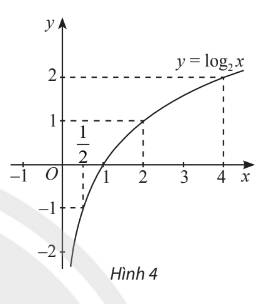
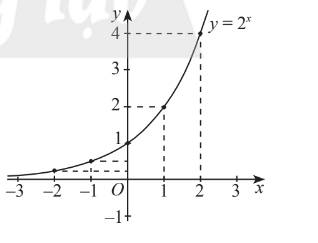
a) Xét hàm số mũ \(y = {2^x}\) với tập xác định \(\mathbb{R}\).
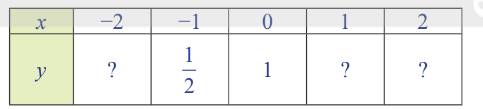
i) Hoàn thành bảng giá trị sau:
ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị hàm số \(y = {2^x}\) như Hình 2. Từ đồ thị nảy, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số này.
i:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/4 | 1/2 | 1 | 2 | 4 |
ii:
Hàm số liên tục và đồng biến trên R
\(\lim\limits_{x\rightarrow+\infty}2^x=+\infty;\lim\limits_{x\rightarrow-\infty}2^x=0\)
Tập giá trị: \((0;+\infty)\)
b:
bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 2 | 1 | 1/2 | 1/4 |
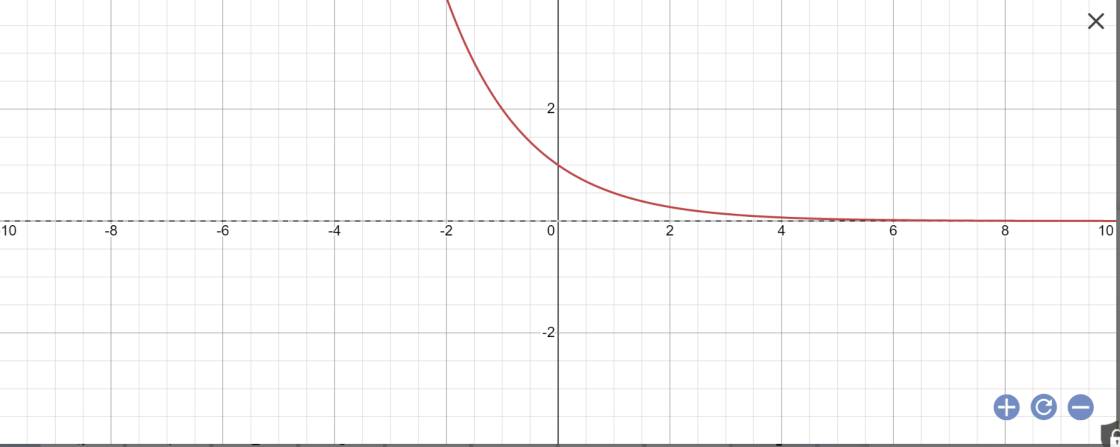
Hàm số liên tục và nghịch biến trên R
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{2}\right)^x=0;\lim\limits_{x\rightarrow-\infty}\left(\dfrac{1}{2}\right)^x=+\infty\)
Tập giá trị: (0;+\(\infty\))