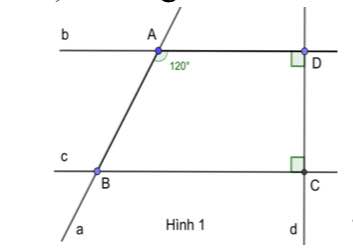
a, Vì b và c cùng vuông góc với d nên b//c
b, Vì b//c nên \(\widehat{A}=\widehat{ABc}=120^0\left(so.le.trong\right);\widehat{A}=\widehat{BCa}=120^0\left(đồng.vị\right)\)
Ta có \(\widehat{ABc}+\widehat{ABC}=180^0\left(kề.bù\right)\Rightarrow\widehat{ABC}=180^0-120^0=60^0\)
Ta có \(\widehat{aBc}=\widehat{ABC}=60^0\left(đối.đỉnh\right)\)
vì b//c
=> \(\widehat{DAB}+\widehat{ABC}=180\) ( 2 góc trong cùng phía bù nhau )
=> \(120+\widehat{ABC}=180=>\widehat{ABC}=60\)
=> \(\widehat{ABC}=\widehat{cBa}=60\) ( đối đỉnh)
\(\widehat{ABC}+\widehat{ABc}=180\) ( 2 góc kề bù)
=> \(60+\widehat{ABc}=180=>\widehat{ABc}=120\)
\(\widehat{ABc}=\widehat{aBC}=120\) đối đỉnh